CF581C Developing Skills

Petya 正在玩一个游戏，主角有 $n$ 个技能，每个技能值 $a_i$ 在 $[0,100]$ 之间，当然技能值越高，技能越强；而主角的综合能力值为 $\sum\left \lfloor \dfrac{a_{i}}{10} \right \rfloor $，其中 $\left \lfloor\right \rfloor$ 为取整运算。 游戏开始时，Petya 有一个技能奖励包，包含 $k$ 点技能提升值，可以给任何一项技能提升一点技能值。现在编程计算 Petya 利用这个奖励包，可以把主角的综合能力值提升到的最大可能值。 注意：每个技能值最多能提升到 $100$。

第一行为正整数 $n(\le 10^5)$ 和 $k(\le10^7)$，第二行为 $n$ 个非负整数 $a_i (≤100)$，以空格隔开，意义如上所述。

对于每组数据，输出游戏主角提升后的最大综合能力值。 by [CRTL_xzh2009](https://www.luogu.com.cn/user/513054)

In the first test case the optimal strategy is as follows. Petya has to improve the first skill to 10 by spending 3 improvement units, and the second skill to 10, by spending one improvement unit. Thus, Petya spends all his improvement units and the total rating of the character becomes equal to $ lfloor\ frac{100}{10}\ rfloor+\ lfloor\ frac{100}{10}\ rfloor=10+10= $ 20. In the second test the optimal strategy for Petya is to improve the first skill to 20 (by spending 3 improvement units) and to improve the third skill to 20 (in this case by spending 1 improvement units). Thus, Petya is left with 4 improvement units and he will be able to increase the second skill to 19 (which does not change the overall rating, so Petya does not necessarily have to do it). Therefore, the highest possible total rating in this example is 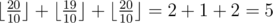. In the third test case the optimal strategy for Petya is to increase the first skill to 100 by spending 1 improvement unit. Thereafter, both skills of the character will be equal to 100, so Petya will not be able to spend the remaining improvement unit. So the answer is equal to 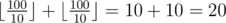.