CF582C Superior Periodic Subarrays

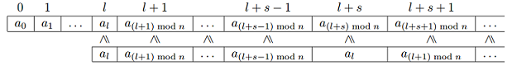
给定一个长度为 $n$ 的无限循环数组 $a_{0},a_{1},...,a_{n-1},...$，其周期长度为 $n$。形式化地，$a_{i}=a_{i\bmod n}$。 数组 $a$ 的一个周期性子数组 $(l, s)$（$0 \leq l < n$，$1 \leq s < n$）是一个周期长度为 $s$ 的无限循环数组，其为 $a$ 的某个长度为 $s$ 的连续子段，从位置 $l$ 开始。 如果一个周期性子数组 $(l,s)$ 满足：当将其从下标 $l$ 开始附加到数组 $a$ 上时，子数组中的任意元素都大于等于 $a$ 中对应位置的元素，则称其为“优越”周期子数组。如下图所示（上方为无限数组 $a$，下方为其周期性子数组 $(l,s)$）：  请你求出有多少组不同的 $(l, s)$ 对应着优越的周期子数组。

第一行输入一个整数 $n$（$1 \leq n \leq 2 \times 10^{5}$）。 第二行输入 $n$ 个整数 $a_{0},a_{1},...,a_{n-1}$（$1 \leq a_{i} \leq 10^{6}$），用空格隔开。

输出一个整数，即满足条件的 $(l, s)$ 对的数量。

在第一个样例中，优越的子数组为 $(0, 1)$ 和 $(3, 2)$。 子数组 $(0, 1)$ 是优越的，因为 $a_{0} \geq a_{0}, a_{0} \geq a_{1}, a_{0} \geq a_{2}, a_{0} \geq a_{3}, a_{0} \geq a_{0},...$ 。 子数组 $(3, 2)$ 是优越的，因为 $a_{3} \geq a_{3}, a_{0} \geq a_{0}, a_{3} \geq a_{1}, a_{0} \geq a_{2}, a_{3} \geq a_{3},...$ 。 在第三个样例中，任意一对 $(l,s)$ 都对应一个优越的子数组，因为数组的所有元素都不同。 由 ChatGPT 5 翻译