CF584B Kolya and Tanya

Kolya 喜欢将侏儒们围坐在圆桌旁并给他们发放硬币，而 Tanya 喜欢研究那些分别坐在等边三角形三个顶点上的侏儒三元组。 更正式地说，有 $3n$ 个侏儒围成一圈就坐。每个侏儒可以拥有 $1$ 到 $3$ 枚硬币。我们对圆桌上的位置从 $0$ 到 $3n-1$ 编号，坐在第 $i$ 号位置的侏儒拥有 $a_{i}$ 枚硬币。如果存在某个整数 $i$（$0 \leq i < n$），使得 $a_{i} + a_{i+n} + a_{i+2n} \neq 6$，那么 Tanya 就会感到满意。 请计算可以让 Tanya 满意的分配方式共有多少种。由于分配方案数可能很大，请输出其对 $10^{9} + 7$ 取模的结果。两个分配方案 $a$ 和 $b$ 被认为不同，当且仅当存在某个 $i$（$0 \leq i < 3n$），满足 $a_{i} \neq b_{i}$（即有侏儒分到的硬币数不同）。

一行包含一个整数 $n$（$1 \leq n \leq 10^{5}$），表示侏儒的数量除以三。

输出一个整数，表示可以让 Tanya 满意的分配方案数对 $10^{9}+7$ 取模的结果。

当 $n=1$ 时共有 $20$ 种方案（编号为 $0$ 的侏儒坐在三角形顶部，$1$ 号在右顶点，$2$ 号在左顶点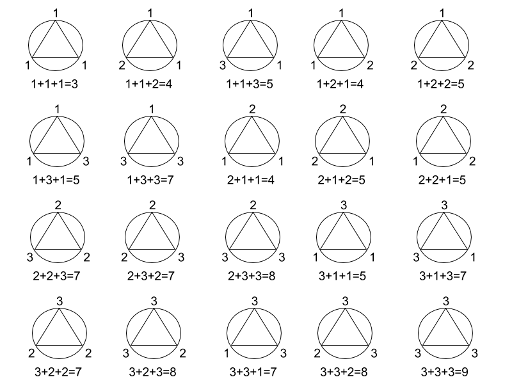）： 由 ChatGPT 5 翻译