CF584B Kolya and Tanya

Kolya loves putting gnomes at the circle table and giving them coins, and Tanya loves studying triplets of gnomes, sitting in the vertexes of an equilateral triangle. More formally, there are $ 3n $ gnomes sitting in a circle. Each gnome can have from $ 1 $ to $ 3 $ coins. Let's number the places in the order they occur in the circle by numbers from $ 0 $ to $ 3n-1 $ , let the gnome sitting on the $ i $ -th place have $ a_{i} $ coins. If there is an integer $ i $ ( $ 0

A single line contains number $ n $ ( $ 1

Print a single number — the remainder of the number of variants of distributing coins that satisfy Tanya modulo $ 10^{9}+7 $ .

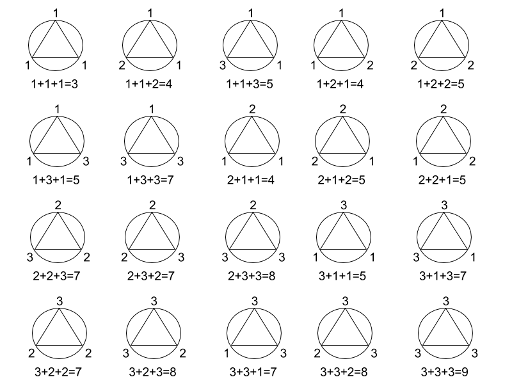
$ 20 $ ways for $ n=1 $ (gnome with index $ 0 $ sits on the top of the triangle, gnome $ 1 $ on the right vertex, gnome $ 2 $ on the left vertex):