CF587B Duff in Beach
题目描述
### 题目翻译
给出一个长度为$n$的序列$a_0,a_1,...,a_{n-1}$,通过它构造出一个长度为$l$的序列$b_0,b_1,...,b_{l-1}$满足$b_i = a_{i \mod n}$。
现求满足如下条件的$b$的子序列$b_{q_0} , b_{q_1},...,b_{q_{x-1}}$的数量:
1、$1 \leq x \leq k$
2、$\forall i \in [0,x-2] , \lfloor\frac{q_i}{n} \rfloor = \lfloor \frac{q_{i+1}}{n} \rfloor -1$
3、$\forall i \in [0,x-2] , b_{q_i} \leq b_{q_{i+1}}$
输入格式
第一行三个正整数 $n,l,k$($n k \leq 10^6$,$l \leq {10}^{18}$)。
接下来一行 $n$ 个正整数 $a_i$($a_i \leq {10}^9$)描述序列。
输出格式
一行一个正整数表示答案模$10^9+7$。
说明/提示
In the first sample case, 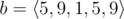. So all such sequences are: 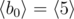, 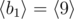, 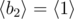, 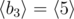, 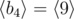, 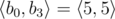, 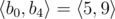, 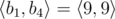, 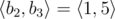 and 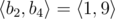.