CF593C Beautiful Function

给出$n$个圆，构造两个合法的函数$f(t),g(t)$，设点集$S$是整数$t\in[0,50]$时$(f(t),g(t))$构成的点的集合，你需要保证对于每一个圆，至少存在一个点（包括边界）在点集$S$中。 令$w(t)$与$h(t)$为两个合法的函数，那么合法的函数由以下几种函数复合而成： ①$s(t) = abs(w(t))$，其中$abs()$表示取绝对值 ②$s(t) = (w(t) + h(t))$ ③$s(t) = (w(t) - h(t))$ ④$s(t) = (w(t) \times h(t))$ ⑤$s(t) = C$（C为整数） ⑥$s(t) = t$ 在$f(t)$与$g(t)$中，只能至多出现$50$次函数相乘的操作，函数长度不能超过$100n$，**输出时不能出现空格**，并且当整数$t \in [0,50]$时，$-10^9 \leq f(t),g(t) \leq 10^9$

第一行一个整数$n(1 \leq n \leq 50)$表示圆的数量 接下来$n$行每行三个整数$x,y,r(0 \leq x , y \leq 50 , 2 \leq r \leq 50)$描述一个圆的坐标与半径。

两行，第一行为$f(x)$，第二行为$g(x)$

Correct functions: 1. $ 10 $ 2. ( $ 1 $ + $ 2 $ ) 3. (( $ t $ - $ 3 $ )+( $ t $ \* $ 4 $ )) 4. $ abs((t $ - $ 10)) $ 5. $ (abs((((23 $ - $ t $ )\*( $ t $ \* $ t $ ))+(( $ 45 $ + $ 12 $ )\*( $ t $ \* $ t)))) $ \* $ ((5 $ \* $ t $ )+(( $ 12 $ \* $ t $ )- $ 13))) $ 6. $ abs((t $ -( $ abs((t $ \* $ 31 $ ))+ $ 14)))) $ Incorrect functions: 1. $ 3 $ + $ 5 $ + $ 7 $ (not enough brackets, it should be (( $ 3 $ + $ 5 $ )+ $ 7 $ ) or ( $ 3 $ +( $ 5 $ + $ 7 $ ))) 2. $ abs(t $ - $ 3) $ (not enough brackets, it should be $ abs((t $ - $ 3)) $ 3. $ 2 $ + $ (2 $ - $ 3 $ (one bracket too many) 4. $ 1 $ ( $ t $ + $ 5 $ ) (no arithmetic operation between 1 and the bracket) 5. $ 5000 $ \* $ 5000 $ (the number exceeds the maximum) 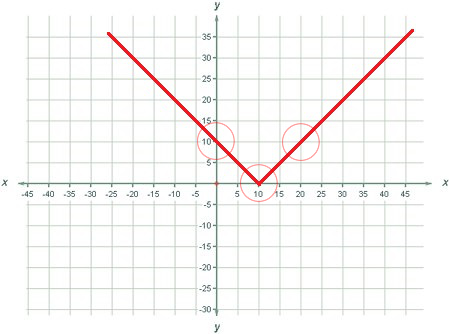 The picture shows one of the possible solutions