CF593D Happy Tree Party
题目描述
为了庆祝博格丹的生日,他的母亲送给他一棵有 $n$ 个节点的树,树的第 $i$ 条边上有一个数字 $x_i$。顺带提醒一下,一棵树指的是一个由无向边连接的无环连通图。在礼物被送出之后,有 $m$ 位访客陆续来到博格丹家中参加派对。第 $i$ 位访客会进行如下两种操作之一:
1. 选择一个数 $y_i$ 和两个节点 $a_i$ 和 $b_i$。在这之后,他会沿着树的边走一遍从 $a_i$ 到 $b_i$ 的最短路(当然,在树上这样的路径只有一条)。每当他经过一条边 $j$ 时,他选择的数 $y_i$ 会立刻变成 $\lfloor \frac{y_i}{x_j} \rfloor$,也就是 $\frac{y_i}{x_j}$ 向下取整。
2. 选择第 $p_i$ 条边 ,把它的边权 $x_{p_i}$ 改为一个正整数 $c_i \in [1,x_{p_i})$。
由于博格丹很替他的客人们着想,他决定简化这个过程。你需要写一个程序处理访客们的操作,并且对于每个第一类操作 $i$,输出 $y_i$ 最后的值。
输入格式
输入的第一行包含两个整数 $n$ 和 $m$($2\le n\le200000$,$1\le m\le200000$),分别表示树的节点数和访客的数量。
接下来 $n-1$ 行描述每一条边的信息。这些行中的第 $i$ 行包含三个整数 $u_i$,$v_i$,$x_i$($1\le u_i,v_i\le n$,$u_i\ne v_i$,$1\le x_i \le 10^{18}$),表示节点 $u_i$ 和 $v_i$ 之间有一条写有 $x_i$ 的无向边。
接下来 $m$ 行描述访客们的操作。每一行包含三或四个整数,操作分为以下两类:
* $1\ a_i\ b_i\ y_i$,表示第一类操作。
* $2\ p_i\ c_i$,表示第二类操作。
你可以认为每一个询问都是合法的,也就是说,$1\le a_i,b_i\le n$,$1\le p_i\le n-1$,$1\le y_i\le10^{18}$ 并且 $1\le c_i< x_{p_i}$,此时的 $x_{p_i}$ 不一定和最开始的 $x_{p_i}$ 相等,因为它可能已经被更新过。所有边按照 $1\sim n-1$ 的标号依次在输入中给出。
输出格式
对于每个第一类操作 $i$,输出一行一个整数,表示从 $a_i$ 走到 $b_i$ 后 $y_i$ 最终的值。
说明/提示
树的初始形态如下:
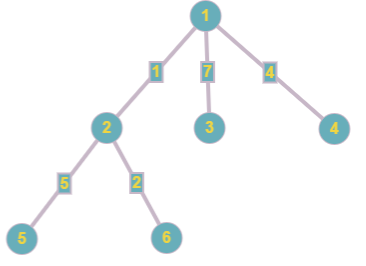
第一个查询的答案是:$\lfloor\frac{\lfloor\frac{17}{4}\rfloor}{2}\rfloor=2$。
更改第三条边后,树的形态如下:
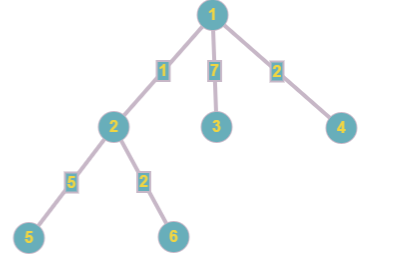
第二个查询的答案是:$\lfloor\frac{\lfloor\frac{17}{2}\rfloor}{2}\rfloor=4$。
在第三个查询中,起点与终点重合,答案为初始数字 $20$。
更改第四条边后,树的形态如下:
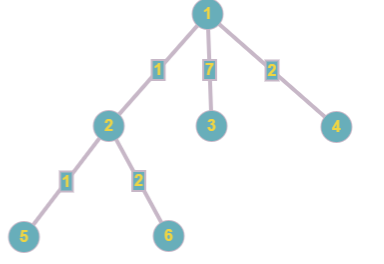
最后一个查询的答案是:$\lfloor\frac{\lfloor\frac{3}{1}\rfloor}{1}\rfloor=3$。