CF594B Max and Bike

几个月以来，Maxim 一直骑着他心爱的自行车上班。最近，他决定参加自行车比赛。 他知道今年将会有 $n$ 场比赛。在第 $i$ 场比赛中，参赛者需要以最快的速度沿着一条直线，从点 $s_i$ 骑到点 $f_i$（$s_i < f_i$）。 计时是一个与特殊传感器和计时器有关的复杂过程。可以将自行车的前轮视为半径为 $r$ 的圆。忽略轮胎的厚度、传感器的大小以及一切物理效应。传感器被安装在轮辋上的某个固定点，也就是圆上某个半径为 $r$ 的点。之后计时器就像这个圆上的指定点一样运动，也就是既会向前移动，又会绕圆心旋转。 出发时，每个参赛者可以选择任意一个点 $b_i$，使得他的自行车完全位于起点线的后方，即 $b_i < s_i - r$。随后他开始运动，即刻加速到最大速度。当传感器的坐标等于起点的坐标时（即时刻 $ts_i$），计时开始。选手以最大速度骑完全程，当传感器的坐标等于终点的坐标时（即时刻 $tf_i$），计时停止，记录最终时间。这样，计时器记录的全程时间是 $tf_i-ts_i$。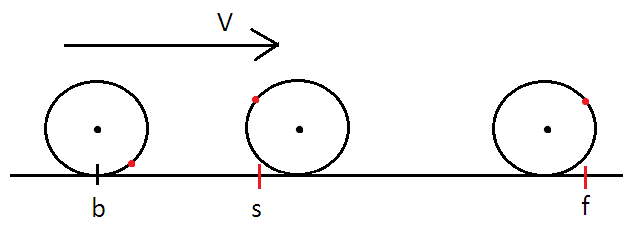  Maxim 数学很好，他怀疑实际用时不仅取决于最大速度 $v$，还和他选择的初始点 $b_i$ 有关。现在 Maxim 想让你帮忙计算每一场比赛计时器所能记录到的最小时间。自行车前轮的半径为 $r$。

第一行包含三个整数 $n$、$r$ 和 $v$（$1 \leq n \leq 100000, 1 \leq r, v \leq 10^{9}$），分别表示比赛场数、自行车前轮的半径以及最大速度。 接下来 $n$ 行，每行两个整数 $s_i$ 和 $f_i$（$1 \leq s_i < f_i \leq 10^{9}$），表示第 $i$ 场比赛的起点和终点坐标。

输出 $n$ 个实数，第 $i$ 个表示第 $i$ 场比赛计时器所能记录到的最小时间。你的答案如果与标准答案的绝对误差或相对误差不超过 $10^{-6}$ 都将被视为正确。 即：假设你的答案为 $a$，评测程序的答案为 $b$，如果满足 $|a-b|/\max(1,|b|) < 10^{-6}$，则判为正确。

由 ChatGPT 5 翻译