CF596D Wilbur and Trees
题目描述
小猪 Wilbur 非常想成为一只海狸,于是他今天决定假装自己是一只海狸,去咬树把它们砍倒。
有 $n$ 棵树分布在一条直线上的不同位置,第 $i$ 棵树位于 $x_i$ 位置。所有树的位置均不相同。
这些树都是一样高,每棵树的高度为 $h$。由于风的影响,当一棵树被砍倒时,以概率 $p$ 向左倒,以概率 $1-p$ 向右倒。如果一棵树在倒下时碰到另一棵树,被碰到的树也会朝相同的方向倒下。只有当两棵树之间的距离严格小于 $h$ 时,才会发生相互碰撞。
例如,假设有 $4$ 棵树分别位于 $1$、$3$、$5$ 和 $8$ 号位置,$h=3$,且 $1$ 号位置的树向右倒。那么它会撞到 $3$ 号位置的树,并使其也倒下,接着又撞到 $5$ 号位置的树,使其也倒下。而 $8$ 号位置的树与 $5$ 号位置的距离恰好是 $3$,因此不会倒下。
只要还有树站立,Wilbur 就会以 $0.5$ 的概率选择最左边还未倒下的树,或以 $0.5$ 的概率选择最右边还未倒下的树来砍倒。如果只剩下一棵树,他总是选择它。由于地面上长满了青草,Wilbur 想知道当他把所有树都砍倒后,倒下的树覆盖在地面上的预期总长度是多少,因为他关心吃草的奶牛朋友们。请你帮助 Wilbur 计算这个期望值。
输入格式
输入的第一行包含两个整数 $n$ ($1 \leq n \leq 2000$) 和 $h$ ($1 \leq h \leq 10^{8}$),以及一个实数 $p$($0 \leq p \leq 1$),小数部分不超过六位。
第二行包含 $n$ 个整数 $x_1, x_2, ..., x_n$,$(-10^8 \leq x_i \leq 10^8)$,顺序任意。
输出格式
输出一个实数——所有树被砍倒后倒下的树覆盖在地面上的期望总长度。若你的答案与标准答案的绝对误差或相对误差不超过 $10^{-6}$,则视为正确。
也就是说,假设你的输出为 $a$,标准答案为 $b$,只要 $|a-b| \leq 10^{-6} \cdot \max(1, |b|)$,则你的答案视为正确。
说明/提示
以第一个示例为例,有两棵树,高度为 $2$。
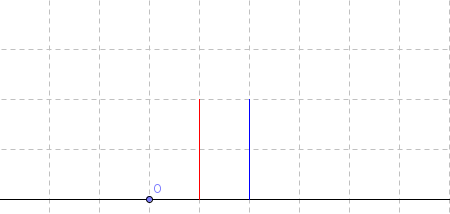
共有三种情况:
1. 两棵树都向左倒。这可能发生在右边那棵树先被砍倒并向左倒,这时会同时撞倒左边的树,概率为 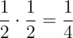;也可能是先砍倒左边的树,然后再砍倒右边的树,两者概率为 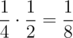。总概率是 。
2. 两棵树都向右倒。这与情况 (1) 类似,总概率同样为 。
3. 左边的树向左倒,右边的树向右倒。这是唯一剩下的情况,概率为 。
第 1、2 种情况总共覆盖 $3$ 个单位长度,第 3 种情况覆盖 $4$ 个单位长度。因此期望为 。
由 ChatGPT 5 翻译