CF599E Sandy and Nuts

有根树是一个无简单环的连通图，其中选定一个顶点作为根。在本题中，顶点 $1$ 始终作为根。 两个顶点 $u$ 和 $v$ 的最近公共祖先（Lowest Common Ancestor，LCA）指的是距离根最远、同时位于从 $u$ 到根和从 $v$ 到根的路径上的顶点。记作 $LCA(u,v)$。 Sandy 有一棵包含 $n$ 个顶点的有根树，用来存储她的坚果。不幸的是，水下风暴摧毁了她的树，她不记得所有的边。她只设法恢复了初始树的 $m$ 条边，以及 $q$ 组三元组 $a_{i}$、$b_{i}$ 和 $c_{i}$，她认为 $LCA(a_{i},b_{i})=c_{i}$。 请帮助 Sandy 统计以 $1$ 号顶点为根、规模为 $n$ 的树，满足所有她记得的信息的方案数。如果她记的信息有误，导致不存在这样的树，则输出 $0$。两棵有根树被认为不同，当且仅当存在一条边仅出现在其中一棵树中。

输入的第一行包含三个整数 $n$、$m$ 和 $q$（$1 \leq n \leq 13, 0 \leq m < n, 0 \leq q \leq 100$），分别表示顶点数、已知边数，以及 Sandy 记得的 $LCA$ 三元组数。 接下来的 $m$ 行，每行包含两个整数 $u_{i}$ 和 $v_{i}$（$1 \leq u_{i}, v_{i} \leq n, u_{i} \ne v_{i}$），表示树中已连接的第 $i$ 条边。保证这些边的集合是某棵树的子集。 最后 $q$ 行，每行包含三个整数 $a_{i}$、$b_{i}$ 和 $c_{i}$（$1 \leq a_{i}, b_{i}, c_{i} \leq n$）。每个三元组表示 $LCA(a_{i}, b_{i}) = c_{i}$。不能保证存在一棵树满足所有给定的 $LCA$ 条件。

输出一个整数，表示满足所有条件的树的数量。

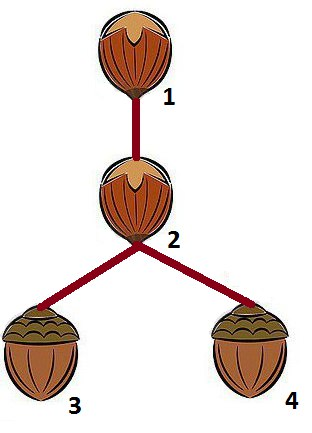
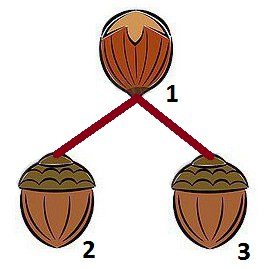
第二个样例的正确答案如下图所示：  第三个样例有两棵可能的树：   第四个样例中，由于 $LCA$ 信息矛盾，答案为 $0$。 由 ChatGPT 5 翻译