CF601A The Two Routes

In Absurdistan, there are $ n $ towns (numbered $ 1 $ through $ n $ ) and $ m $ bidirectional railways. There is also an absurdly simple road network — for each pair of different towns $ x $ and $ y $ , there is a bidirectional road between towns $ x $ and $ y $ if and only if there is no railway between them. Travelling to a different town using one railway or one road always takes exactly one hour. A train and a bus leave town $ 1 $ at the same time. They both have the same destination, town $ n $ , and don't make any stops on the way (but they can wait in town $ n $ ). The train can move only along railways and the bus can move only along roads. You've been asked to plan out routes for the vehicles; each route can use any road/railway multiple times. One of the most important aspects to consider is safety — in order to avoid accidents at railway crossings, the train and the bus must not arrive at the same town (except town $ n $ ) simultaneously. Under these constraints, what is the minimum number of hours needed for both vehicles to reach town $ n $ (the maximum of arrival times of the bus and the train)? Note, that bus and train are not required to arrive to the town $ n $ at the same moment of time, but are allowed to do so.

The first line of the input contains two integers $ n $ and $ m $ ( $ 2

Output one integer — the smallest possible time of the later vehicle's arrival in town $ n $ . If it's impossible for at least one of the vehicles to reach town $ n $ , output $ -1 $ .

In the first sample, the train can take the route 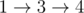 and the bus can take the route 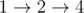. Note that they can arrive at town $ 4 $ at the same time. In the second sample, Absurdistan is ruled by railwaymen. There are no roads, so there's no way for the bus to reach town $ 4 $ .