CF601D Acyclic Organic Compounds

给定一棵有 $n$ 个结点的树 $T$（结点编号为 $1$ 到 $n$），每个结点上标有一个字母。该树以结点 $1$ 作为根。 对于某个结点 $v$ 的子树 $T_v$，可以沿着从 $v$ 出发，经过简单路径到达 $T_v$ 中某个结点（可以是 $v$ 本身）的路径，读取一个字符串。我们用 $F(v)$ 表示能通过上述方式读取到的不同字符串的数量。 每个结点 $v$ 都有一个权值 $c_v$。我们关注 $F(v) + c_v$ 值最大的那些结点。 请你计算两个统计量：所有 $1 \leq v \leq n$ 的 $F(v)+c_v$ 的最大值，以及取到最大值的结点数。

第一行包含一个整数 $n$（$1 \leq n \leq 300000$）——树的结点数。 第二行包含 $n$ 个用空格分隔的整数 $c_i$（$0 \leq c_i \leq 10^{9}$）。 第三行包含一个长度为 $n$ 的小写英文字母字符串 $s$，第 $i$ 个字符为结点 $i$ 上的字母。 接下来的 $n-1$ 行，每行包含两个用空格分隔的整数 $u$ 和 $v$（$1 \leq u,v \leq n$），表示树中一条连接 $u$ 和 $v$ 的边。 保证输入数据描述的是一棵树。

输出两行。 第一行输出所有 $1 \leq v \leq n$ 的 $F(v)+c_v$ 的最大值。 第二行输出取得最大值的结点数量。

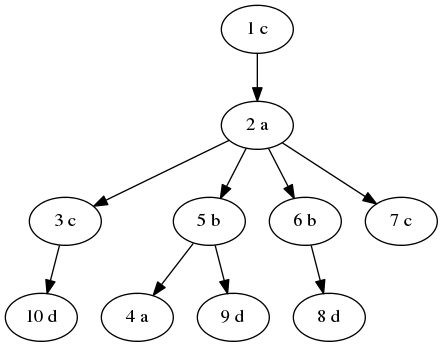
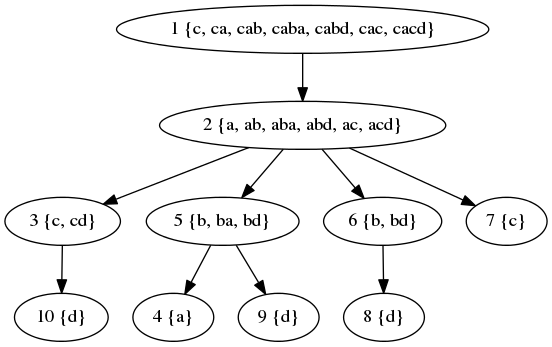
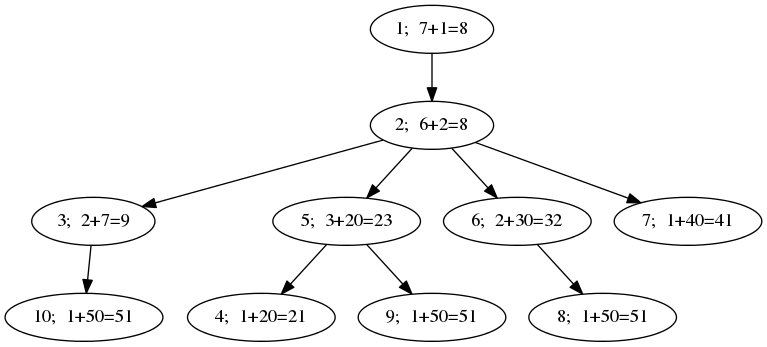
在第一个样例中，树的结构如下：  各个结点可读取的字符串集合如下：  最终各结点的 $F(v)+c_v$ 值为：  在第二个样例中，各结点的 $F(v)+c_v$ 值为 $ (5,4,2,1,1,1) $。在 $T_2$ 的不同字符串为 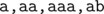；注意 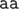 可以分别通过到结点 $3$ 或 $4$ 的两条路径得到。 由 ChatGPT 5 翻译