CF601E A Museum Robbery

There's a famous museum in the city where Kleofáš lives. In the museum, $ n $ exhibits (numbered $ 1 $ through $ n $ ) had been displayed for a long time; the $ i $ -th of those exhibits has value $ v_{i} $ and mass $ w_{i} $ . Then, the museum was bought by a large financial group and started to vary the exhibits. At about the same time, Kleofáš... gained interest in the museum, so to say. You should process $ q $ events of three types: - type $ 1 $ — the museum displays an exhibit with value $ v $ and mass $ w $ ; the exhibit displayed in the $ i $ -th event of this type is numbered $ n+i $ (see sample explanation for more details) - type $ 2 $ — the museum removes the exhibit with number $ x $ and stores it safely in its vault - type $ 3 $ — Kleofáš visits the museum and wonders (for no important reason at all, of course): if there was a robbery and exhibits with total mass at most $ m $ were stolen, what would their maximum possible total value be? For each event of type 3, let $ s(m) $ be the maximum possible total value of stolen exhibits with total mass $

The first line of the input contains two space-separated integers $ n $ and $ k $ ( $ 1

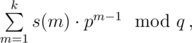As the number of values $ s(m) $ can get large, output the answers to events of type 3 in a special format. For each event of type 3, consider the values $ s(m) $ computed for the question that Kleofáš asked in this event; print one line containing a single number where $ p=10^{7}+19 $ and $ q=10^{9}+7 $ . Print the answers to events of type 3 in the order in which they appear in the input.

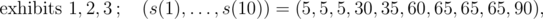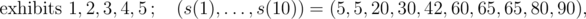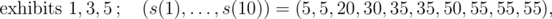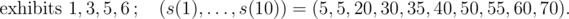In the first sample, the numbers of displayed exhibits and values $ s(1),...,s(10) $ for individual events of type 3 are, in order:    The values of individual exhibits are $ v_{1}=30,v_{2}=60,v_{3}=5,v_{4}=42,v_{5}=20,v_{6}=40 $ and their masses are $ w_{1}=4,w_{2}=6,w_{3}=1,w_{4}=5,w_{5}=3,w_{6}=6 $ . In the second sample, the only question is asked after removing all exhibits, so $ s(m)=0 $ for any $ m $ .