CF603B Moodular Arithmetic

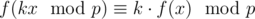
作为一名聪明的学生，Kevin Sun 在 Bovinia State University (BGU) 跟随 Farmer Ivan 学习“psyco wlogy”，“cowculus” 和“cryptcowgraphy”。在“Mathematics of Olympiads (MoO)”课上，Kevin 遇到了一个奇怪的函数方程，需要你的帮助。对于两个固定整数 $k$ 和 $p$，其中 $p$ 是一个奇素数，函数方程如下：  这里 $f$ 是某个函数。（该方程对于 $x$ 的任意取值 $0$ 到 $p-1$ 都成立。） 实际上，$f$ 可以有多种不同的取法。Kevin 并不需要你求出某个具体的解，而是想让你计算满足上述方程的不同函数 $f$ 的个数。由于答案可能非常大，请你输出结果对 $10^{9}+7$ 取模后的值。

输入共一行，包含两个用空格分隔的整数 $p$ 和 $k$，满足 $3 \leq p \leq 1000000$，$0 \leq k \leq p-1$。保证 $p$ 是一个奇素数。

输出一个整数，表示满足条件的不同函数 $f$ 的数量，对 $10^{9} + 7$ 取模。

在第一个样例中，$p=3$，$k=2$。以下函数均满足要求： 1. $f(0)=0$，$f(1)=1$，$f(2)=2$。 2. $f(0)=0$，$f(1)=2$，$f(2)=1$。 3. $f(0)=f(1)=f(2)=0$。 由 ChatGPT 5 翻译