CF610C Harmony Analysis

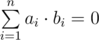
学期已经接近尾声，于是 Danil 决定努力一把，去上一节和声分析课，至少要知道教授长什么样。Danil 在课堂上感到非常无聊，直到老师给大家布置了一个简单的任务：在 $4$ 维空间中找到 $4$ 个向量，使得每个向量的每个坐标只可能是 $1$ 或 $-1$，并且任意两个向量都是正交的。作为提示，在 $n$ 维空间中，如果两个向量的数量积等于零，它们就被认为是正交的，即：  Danil 很快便解决了老师布置的问题，老师指出，对于 $2^k$ 个向量和 $2^k$ 维空间，这个问题也可以解决。当 Danil 回到家后，他也迅速找到了这个一般性问题的解法。你能解决它吗？

输入仅一行，包含一个整数 $k$（$0 \leq k \leq 9$）。

输出 $2^k$ 行，每行包含 $2^k$ 个字符。第 $i$ 行第 $j$ 个字符为“$*$”当第 $i$ 个向量的第 $j$ 个坐标为 $-1$，为“$+$”当该坐标为 $+1$。保证一定有解。 如果有多个正确答案，输出任意一个均可。

考虑示例中的所有数量积： - 向量 $1$ 和 $2$ ：$ (+1)\cdot(+1) + (+1)\cdot(-1) + (-1)\cdot(+1) + (-1)\cdot(-1) = 0$ - 向量 $1$ 和 $3$ ：$ (+1)\cdot(+1) + (+1)\cdot(+1) + (-1)\cdot(+1) + (-1)\cdot(+1) = 0$ - 向量 $1$ 和 $4$ ：$ (+1)\cdot(+1) + (+1)\cdot(-1) + (-1)\cdot(-1) + (-1)\cdot(+1) = 0$ - 向量 $2$ 和 $3$ ：$ (+1)\cdot(+1) + (-1)\cdot(+1) + (+1)\cdot(+1) + (-1)\cdot(+1) = 0$ - 向量 $2$ 和 $4$ ：$ (+1)\cdot(+1) + (-1)\cdot(-1) + (+1)\cdot(-1) + (-1)\cdot(+1) = 0$ - 向量 $3$ 和 $4$ ：$ (+1)\cdot(+1) + (+1)\cdot(-1) + (+1)\cdot(-1) + (+1)\cdot(+1) = 0$。 由 ChatGPT 5 翻译