CF611C New Year and Domino

They say "years are like dominoes, tumbling one after the other". But would a year fit into a grid? I don't think so. Limak is a little polar bear who loves to play. He has recently got a rectangular grid with $ h $ rows and $ w $ columns. Each cell is a square, either empty (denoted by '.') or forbidden (denoted by '\#'). Rows are numbered $ 1 $ through $ h $ from top to bottom. Columns are numbered $ 1 $ through $ w $ from left to right. Also, Limak has a single domino. He wants to put it somewhere in a grid. A domino will occupy exactly two adjacent cells, located either in one row or in one column. Both adjacent cells must be empty and must be inside a grid. Limak needs more fun and thus he is going to consider some queries. In each query he chooses some rectangle and wonders, how many way are there to put a single domino inside of the chosen rectangle?

The first line of the input contains two integers $ h $ and $ w $ ( $ 1

Print $ q $ integers, $ i $ -th should be equal to the number of ways to put a single domino inside the $ i $ -th rectangle.

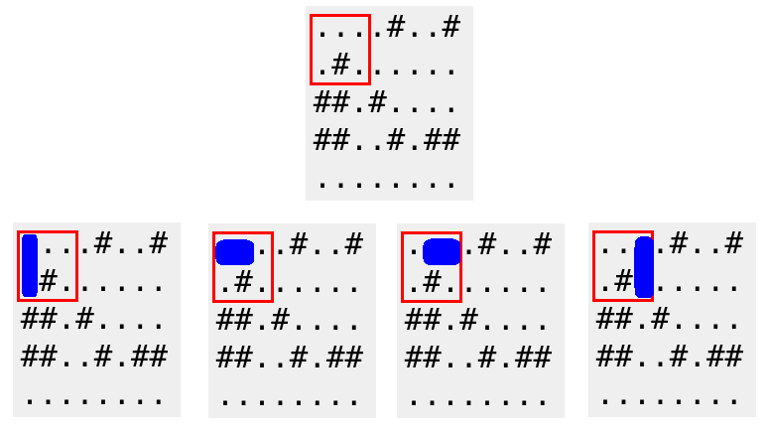
A red frame below corresponds to the first query of the first sample. A domino can be placed in 4 possible ways.