CF617C Watering Flowers

一个花坛中有许多花和两个喷泉。 你可以调整水压，将第一个喷泉和第二个喷泉的喷水半径分别设定为任意的 $r_1\ (r_1 \geq 0)$ 和 $r_2\ (r_2 \geq 0)$，也就是水能喷射到的距离。你需要选定合适的 $r_1$ 和 $r_2$，使得所有的花都能被浇到水。具体来说，对于每一朵花，花到第一个喷泉的距离不超过 $r_1$，或者到第二个喷泉的距离不超过 $r_2$。允许有些花同时被两个喷泉浇到。 你需要尽可能减少用水量，也就是选择 $r_1$ 和 $r_2$，使得所有的花都被浇到且 $r_1^2 + r_2^2$ 的值最小。请你输出这个最小值。

输入的第一行包含整数 $n, x_1, y_1, x_2, y_2$，分别表示花的数量、第一个喷泉的横坐标和纵坐标、第二个喷泉的横坐标和纵坐标（$1 \leq n \leq 2000$, $-10^7 \leq x_1, y_1, x_2, y_2 \leq 10^7$）。 接下来有 $n$ 行，每行包含两个整数 $x_i, y_i$，表示第 $i$ 朵花的横纵坐标（$-10^7 \leq x_i, y_i \leq 10^7$）。 保证输入中的所有 $n+2$ 个点都是不同的。

输出 $r_1^2 + r_2^2$ 的最小可能值。注意，本题中最优答案一定是整数。

第一个样例为（$r_1^2 = 5$，$r_2^2 = 1$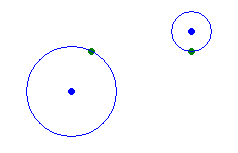）： 第二个样例为（$r_1^2 = 1$，$r_2^2 = 32$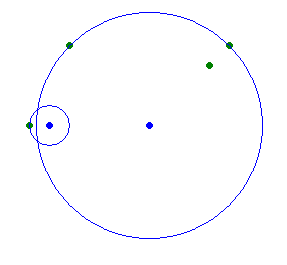）： 由 ChatGPT 5 翻译