CF617C Watering Flowers

A flowerbed has many flowers and two fountains. You can adjust the water pressure and set any values $ r_{1}(r_{1}>=0) $ and $ r_{2}(r_{2}>=0) $ , giving the distances at which the water is spread from the first and second fountain respectively. You have to set such $ r_{1} $ and $ r_{2} $ that all the flowers are watered, that is, for each flower, the distance between the flower and the first fountain doesn't exceed $ r_{1} $ , or the distance to the second fountain doesn't exceed $ r_{2} $ . It's OK if some flowers are watered by both fountains. You need to decrease the amount of water you need, that is set such $ r_{1} $ and $ r_{2} $ that all the flowers are watered and the $ r_{1}^{2}+r_{2}^{2} $ is minimum possible. Find this minimum value.

The first line of the input contains integers $ n $ , $ x_{1} $ , $ y_{1} $ , $ x_{2} $ , $ y_{2} $ ( $ 1

Print the minimum possible value $ r_{1}^{2}+r_{2}^{2} $ . Note, that in this problem optimal answer is always integer.

The first sample is ( $ r_{1}^{2}=5 $ , $ r_{2}^{2}=1 $ ): 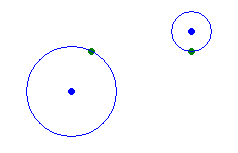 The second sample is ( $ r_{1}^{2}=1 $ , $ r_{2}^{2}=32 $ ):