CF618E Robot Arm
题目描述
Roger 是一个机器人。他有一只手臂,由 $n$ 段连接而成。第 $i$ 段的两个端点初始时分别位于点 $(i-1,0)$ 和 $(i,0)$。对于所有的段,第 $i$ 段的端点 $(i-1,0)$ 被标记为红色,端点 $(i,0)$ 被标记为蓝色。因此,对于所有合法的 $i$,第 $i$ 段的蓝色端点与第 $(i+1)$ 段的红色端点重合。
Roger 可以通过两种方式移动手臂:
1. 他可以选择某一段和一个数值(选择第 $i$ 段以及一个正整数 $l$)。此操作如下:第 $i$ 段的红色端点和第 $1$ 至第 $i-1$ 段都保持不动。设想从红色端点指向蓝色端点的一条射线,蓝色端点以及第 $i+1$ 段到第 $n$ 段一起沿着该射线方向平移 $l$ 个单位长度。
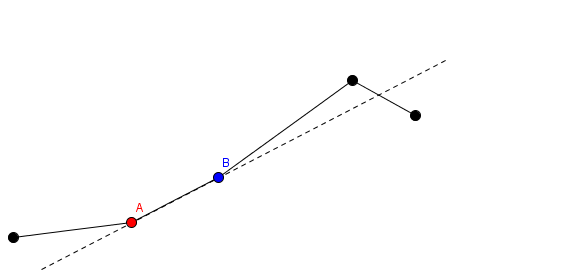
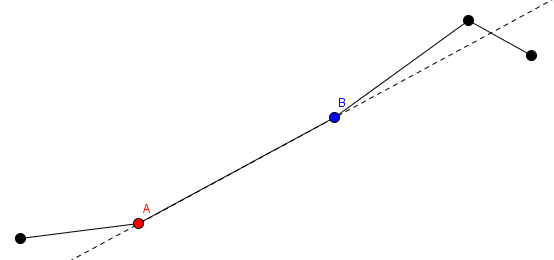
在上图中,标号为 $A$ 的红点以及它之前的段保持位置不变,标号为 $B$ 的蓝点和 $B$ 之后的段被平移。
2. 他可以选择某一段并对其旋转(选择第 $i$ 段及一个角度 $a$)。此操作是:第 $i$ 段的红色端点保持不动,而该段的蓝色端点及第 $i+1$ 到第 $n$ 段围绕该红色端点顺时针旋转 $a$ 度。
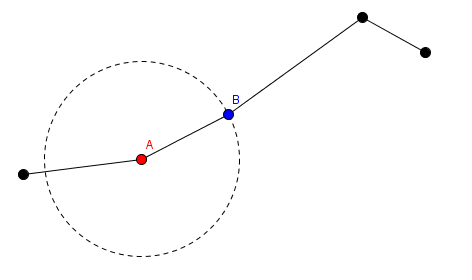
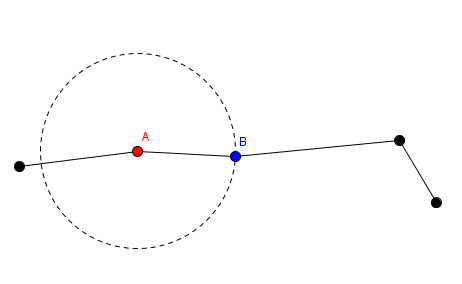
在上图中,标号为 $A$ 的红点和它之前的段保持位置不动,标号为 $B$ 的蓝点和 $B$ 之后的段围绕 $A$ 点旋转。
Roger 需要进行 $m$ 次移动。由于这些变换较为复杂,Roger 很容易忘记最后一段蓝色端点的位置。请你帮他在每次操作后计算最后一段蓝色端点的坐标。注意,这些操作是累计进行的,Roger 的手臂在操作过程中可以任意相交。
输入格式
第一行包含两个整数 $n$ 和 $m$,表示手臂的段数和操作次数($1\leq n,m\leq 300000$)。
接下来 $m$ 行,每行包含三个整数 $x_i$,$y_i$,$z_i$,表示一次操作。
- 如果 $x_i=1$,为第 $1$ 类操作,此时 $y_i$ 表示段号,$z_i$ 表示伸长的长度。
- 如果 $x_i=2$,为第 $2$ 类操作,此时 $y_i$ 表示段号,$z_i$ 表示顺时针旋转的角度(度)。
($1 \leq x_i \leq 2,\, 1 \leq y_i \leq n,\, 1 \leq z_i \leq 359$)
输出格式
输出 $m$ 行。第 $i$ 行输出两个实数,表示经过前 $i$ 次操作后,最后一段蓝色端点的坐标。
你的答案如果与标准答案在绝对误差或相对误差 $10^{-4}$ 以内都算正确。
即,假设某一坐标你的答案为 $a$,标准答案为 $b$,那么如果
$$
\frac{|a-b|}{\max(1, |b|)}
说明/提示
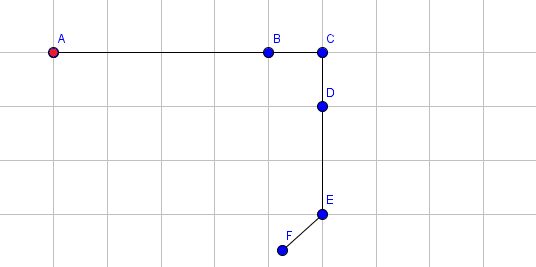
下图展示了每次操作后的手臂状态。每次操作后输出点 $F$ 的坐标。为了简明起见,只画出了每段的蓝色端点(除了第一段的红色端点)。例如,标号为 $B$ 的点是第 $1$ 段的蓝色端点,同时也是第 $2$ 段的红色端点。
初始状态:
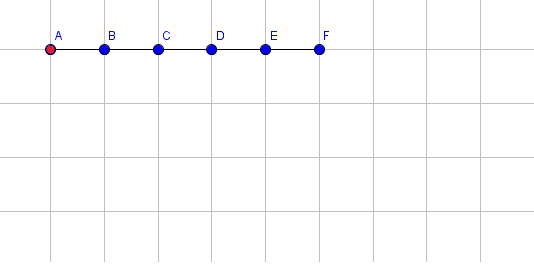
将第 $1$ 段伸长 $3$ 个单位。
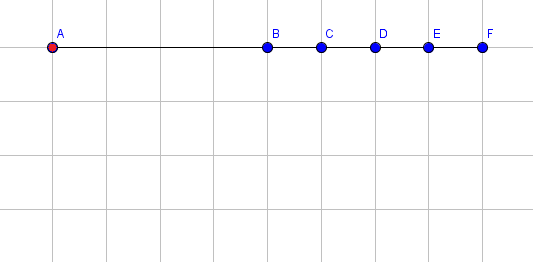
将第 $3$ 段顺时针旋转 $90$ 度。
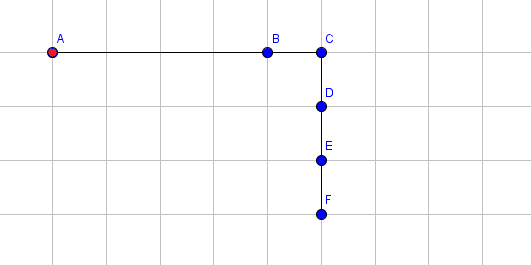
将第 $5$ 段顺时针旋转 $48$ 度。
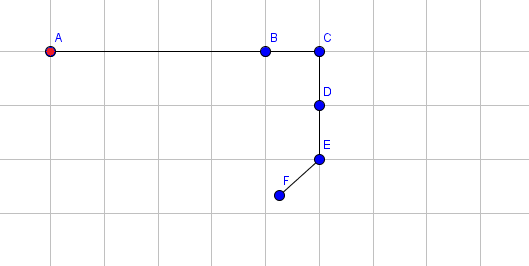
将第 $4$ 段伸长 $1$ 个单位。
由 ChatGPT 5 翻译