CF633D Fibonacci-ish

Yash 最近学习了斐波那契数列，并对此感到非常兴奋。他将一个数列称为“类斐波那契数列”，如果满足以下条件： 1. 数列至少包含两个元素； 2. $f_0$ 和 $f_1$ 可以为任意值； 3. 对于所有 $n\geq 0$，都有 $f_{n+2} = f_{n+1} + f_n$。 给定一个整数序列 $a_1, a_2, \ldots, a_n$，你的任务是重新排列该序列的元素，使得其最长的前缀是一个类斐波那契数列。

输入的第一行包含一个整数 $n$（$2 \leq n \leq 1000$），表示序列 $a_i$ 的长度。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$|a_i| \leq 10^9$）。

输出重新排列后，序列的最长类斐波那契前缀的长度。

在第一个样例中，如果我们把序列排列为 $-1$，$2$，$1$，整个序列 $a_i$ 就是一个类斐波那契数列。 在第二个样例中，最优的排列方式为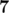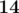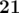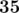：，，，，$28$。 由 ChatGPT 5 翻译