CF638A Home Numbers

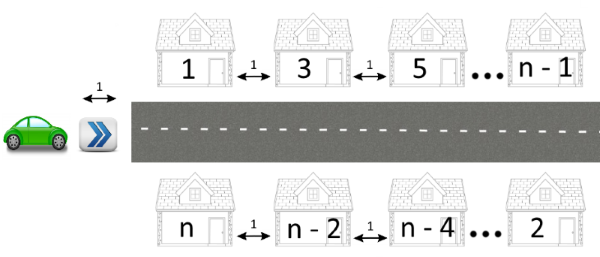
Berland 的主街是一条直线，沿路建有 $n$ 栋房屋（$n$ 是偶数）。房屋分布在街道的两侧。奇数编号的房子在街道的一侧，从街道的起点到终点依次编号为 $1$ 到 $n-1$（如图，从左到右）。偶数编号的房子位于另一侧，从街道的终点到起点依次编号为 $2$ 到 $n$（如图，从右到左）。编号为偶数和奇数的对应房屋彼此正对，即 $1$ 号房对着 $n$ 号房，$3$ 号房对着 $n-2$ 号房，$5$ 号房对着 $n-4$ 号房，以此类推。  Vasya 需要尽快到达编号为 $a$ 的房子。他从街道的起点出发，驾驶汽车前往 $a$ 号房。从街道起点开到 $1$ 号房和 $n$ 号房，均需恰好 $1$ 秒。每经过两座相邻的房子，也同样需要 $1$ 秒。Vasya 可以选择停在任意一侧，因此，对于正对的房子来说，从街道起点到达的距离应视为相同。 你的任务是：求出 Vasya 从街道起点到达 $a$ 号房所需的最少时间。

输入第一行为两个整数 $n$ 和 $a$（$1 \leq a \leq n \leq 100000$）——街道上的房子总数，以及 Vasya 需要到达的房子编号。保证 $n$ 为偶数。

输出一行一个整数，表示 Vasya 从街道起点到 $a$ 号房所需的最少时间。

在第一个样例中，街道上只有四栋房屋，每侧各两栋。$2$ 号房是 Vasya 右手边的最后一栋房屋。 第二个样例对应于 $n=8$ 的情况。$5$ 号房是 Vasya 左手边的倒数第二栋房屋。 由 ChatGPT 5 翻译