CF639B Bear and Forgotten Tree 3

一棵树是一个包含 $n$ 个顶点和 $n-1$ 条边的连通无向图。顶点编号为 $1$ 到 $n$。 Limak 是一只小北极熊，Radewoosh 是他的邪恶敌人。Limak 曾经有一棵树，但 Radewoosh 把它偷走了。现在北极熊很伤心，因为他对树的记忆不深——他只能告诉你三个数 $n$，$d$ 和 $h$： - 这棵树恰好有 $n$ 个顶点。 - 这棵树的直径是 $d$。换句话说，$d$ 是任意两点之间的最大距离。 - Limak 还记得他曾将树以顶点 $1$ 作为根，此时树的高度为 $h$。换句话说，$h$ 是从顶点 $1$ 到其他任意一点的最大距离。 树上两个顶点之间的距离是它们之间简单路径上的边数。 请帮助 Limak 恢复他的树。判断是否存在满足所给条件的树，并随意输出其中一种方案。如果不存在满足条件的树，则输出 $-1$。

第一行包含三个整数 $n$、$d$ 和 $h$（$2 \le n \le 100000,\, 1 \le h \le d \le n-1$）——顶点数、直径、以 $1$ 为根的树的高度。

如果不存在满足 Limak 描述的树，只需输出一行 “-1”。 否则，描述一个满足条件的树。输出 $n-1$ 行，每行输出两个用空格分隔的整数，表示一条树的边所连接的顶点。对于满足条件的多解，输出任意一种即可。边的顺序不限。

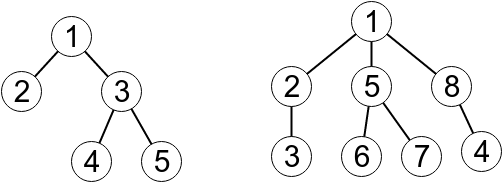
下图展示了第一个样例和第三个样例输出的树。  由 ChatGPT 5 翻译