CF639C Bear and Polynomials

Limak is a little polar bear. He doesn't have many toys and thus he often plays with polynomials. He considers a polynomial valid if its degree is $ n $ and its coefficients are integers not exceeding $ k $ by the absolute value. More formally: Let $ a_{0},a_{1},...,a_{n} $ denote the coefficients, so 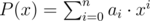. Then, a polynomial $ P(x) $ is valid if all the following conditions are satisfied: - $ a_{i} $ is integer for every $ i $ ; - $ |a_{i}|

The first line contains two integers $ n $ and $ k $ ( $ 1

Print the number of ways to change one coefficient to get a valid polynomial $ Q $ that $ Q(2)=0 $ .

In the first sample, we are given a polynomial $ P(x)=10-9x-3x^{2}+5x^{3} $ . Limak can change one coefficient in three ways: 1. He can set $ a_{0}=-10 $ . Then he would get $ Q(x)=-10-9x-3x^{2}+5x^{3} $ and indeed $ Q(2)=-10-18-12+40=0 $ . 2. Or he can set $ a_{2}=-8 $ . Then $ Q(x)=10-9x-8x^{2}+5x^{3} $ and indeed $ Q(2)=10-18-32+40=0 $ . 3. Or he can set $ a_{1}=-19 $ . Then $ Q(x)=10-19x-3x^{2}+5x^{3} $ and indeed $ Q(2)=10-38-12+40=0 $ . In the second sample, we are given the same polynomial. This time though, $ k $ is equal to $ 12 $ instead of $ 10^{9} $ . Two first of ways listed above are still valid but in the third way we would get $ |a_{1}|>k $ what is not allowed. Thus, the answer is $ 2 $ this time.