CF641F Little Artem and 2-SAT

小 Artem 是一位非常聪明的程序员。他掌握了许多不同的复杂算法。最近他学会了 2-SAT 算法。 在计算机科学中，2-可满足性（简称 2-SAT）是判断一个合取式（逻辑与）由析取式（逻辑或）组成的公式是否有解的特殊情形，其中每个析取式包含不超过两个变量。对于本题，我们只考虑每个析取式恰好包含两个变量的 2-SAT 公式。 例如，如下是一个 2-SAT 问题示例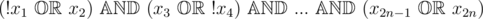：。注意在 2-SAT 公式中可能会出现变量的取反（例如 $x_{1}$ 和 $x_{4}$）的情况。 现在，Artem 尝试解决尽可能多的 2-SAT 问题。他发现了一个非常有趣但目前无法解决的问题。当然，他请求你来帮助他。 问题如下：给定两个 2-SAT 公式 $f$ 和 $g$，判断它们的可行解集合是否完全相同。如果不同，请找出任意一个变量赋值 $x$ 使得 $f(x) \ne g(x)$。

输入的第一行包含三个整数 $n$、$m_{1}$ 和 $m_{2}$（$1 \leq n \leq 1000$，$1 \leq m_{1}, m_{2} \leq n^{2}$），分别表示变量的个数、公式 $f$ 中析取式的数量以及公式 $g$ 中析取式的数量。 接下来 $m_{1}$ 行描述 2-SAT 公式 $f$，每行包含一对整数 $x_{i}$（$-n \leq x_{i} \leq n, x_{i} \ne 0$），$x_{i} > 0$ 表示变量本身，$x_{i} < 0$ 表示变量取反。每一对整数对应一个析取式。 接下来的 $m_{2}$ 行，以相同格式描述 2-SAT 公式 $g$。

如果两个公式的可行解集合完全相同，输出一行单词 “SIMILAR” （不带引号）。否则输出恰好 $n$ 个整数 $x_{i}$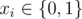（），表示任意一个使 $f(x) \ne g(x)$ 的变量赋值。

第一个样例中的两个公式完全相同，因此它们的可行解集合也完全相同，定义上称为 SIMILAR。 第二个样例中，如果我们令 $x_1 = 0$ 且 $x_2 = 0$，计算第一个函数的值为 $0$，因为 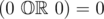。但第二个公式的值为 $1$，因为 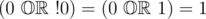。 由 ChatGPT 5 翻译