CF641F Little Artem and 2-SAT

Little Artem is a very smart programmer. He knows many different difficult algorithms. Recently he has mastered in 2-SAT one. In computer science, 2-satisfiability (abbreviated as 2-SAT) is the special case of the problem of determining whether a conjunction (logical AND) of disjunctions (logical OR) have a solution, in which all disjunctions consist of no more than two arguments (variables). For the purpose of this problem we consider only 2-SAT formulas where each disjunction consists of exactly two arguments. Consider the following 2-SAT problem as an example: 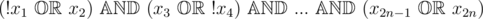. Note that there might be negations in 2-SAT formula (like for $ x_{1} $ and for $ x_{4} $ ). Artem now tries to solve as many problems with 2-SAT as possible. He found a very interesting one, which he can not solve yet. Of course, he asks you to help him. The problem is: given two 2-SAT formulas $ f $ and $ g $ , determine whether their sets of possible solutions are the same. Otherwise, find any variables assignment $ x $ such that $ f(x)≠g(x) $ .

The first line of the input contains three integers $ n $ , $ m_{1} $ and $ m_{2} $ ( $ 1

If both formulas share the same set of solutions, output a single word "SIMILAR" (without quotes). Otherwise output exactly $ n $ integers $ x_{i} $ (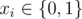) — any set of values $ x $ such that $ f(x)≠g(x) $ .

First sample has two equal formulas, so they are similar by definition. In second sample if we compute first function with $ x_{1}=0 $ and $ x_{2}=0 $ we get the result $ 0 $ , because 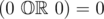. But the second formula is $ 1 $ , because 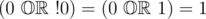.