CF643A Bear and Colors

Bear Limak has $ n $ colored balls, arranged in one long row. Balls are numbered $ 1 $ through $ n $ , from left to right. There are $ n $ possible colors, also numbered $ 1 $ through $ n $ . The $ i $ -th ball has color $ t_{i} $ . For a fixed interval (set of consecutive elements) of balls we can define a dominant color. It's a color occurring the biggest number of times in the interval. In case of a tie between some colors, the one with the smallest number (index) is chosen as dominant. There are 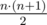 non-empty intervals in total. For each color, your task is to count the number of intervals in which this color is dominant.

The first line of the input contains a single integer $ n $ ( $ 1

Print $ n $ integers. The $ i $ -th of them should be equal to the number of intervals where $ i $ is a dominant color.

In the first sample, color $ 2 $ is dominant in three intervals: - An interval $ [2,2] $ contains one ball. This ball's color is $ 2 $ so it's clearly a dominant color. - An interval $ [4,4] $ contains one ball, with color $ 2 $ again. - An interval $ [2,4] $ contains two balls of color $ 2 $ and one ball of color $ 1 $ . There are $ 7 $ more intervals and color $ 1 $ is dominant in all of them.