CF643B Bear and Two Paths

Bearland has $ n $ cities, numbered $ 1 $ through $ n $ . Cities are connected via bidirectional roads. Each road connects two distinct cities. No two roads connect the same pair of cities. Bear Limak was once in a city $ a $ and he wanted to go to a city $ b $ . There was no direct connection so he decided to take a long walk, visiting each city exactly once. Formally: - There is no road between $ a $ and $ b $ . - There exists a sequence (path) of $ n $ distinct cities $ v_{1},v_{2},...,v_{n} $ that $ v_{1}=a $ , $ v_{n}=b $ and there is a road between $ v_{i} $ and $ v_{i+1} $ for . On the other day, the similar thing happened. Limak wanted to travel between a city $ c $ and a city $ d $ . There is no road between them but there exists a sequence of $ n $ distinct cities $ u_{1},u_{2},...,u_{n} $ that $ u_{1}=c $ , $ u_{n}=d $ and there is a road between $ u_{i} $ and $ u_{i+1} $ for . Also, Limak thinks that there are at most $ k $ roads in Bearland. He wonders whether he remembers everything correctly. Given $ n $ , $ k $ and four distinct cities $ a $ , $ b $ , $ c $ , $ d $ , can you find possible paths $ (v_{1},...,v_{n}) $ and $ (u_{1},...,u_{n}) $ to satisfy all the given conditions? Find any solution or print -1 if it's impossible.

The first line of the input contains two integers $ n $ and $ k $ ( $ 4

Print -1 if it's impossible to satisfy all the given conditions. Otherwise, print two lines with paths descriptions. The first of these two lines should contain $ n $ distinct integers $ v_{1},v_{2},...,v_{n} $ where $ v_{1}=a $ and $ v_{n}=b $ . The second line should contain $ n $ distinct integers $ u_{1},u_{2},...,u_{n} $ where $ u_{1}=c $ and $ u_{n}=d $ . Two paths generate at most $ 2n-2 $ roads: $ (v_{1},v_{2}),(v_{2},v_{3}),...,(v_{n-1},v_{n}),(u_{1},u_{2}),(u_{2},u_{3}),...,(u_{n-1},u_{n}) $ . Your answer will be considered wrong if contains more than $ k $ distinct roads or any other condition breaks. Note that $ (x,y) $ and $ (y,x) $ are the same road.

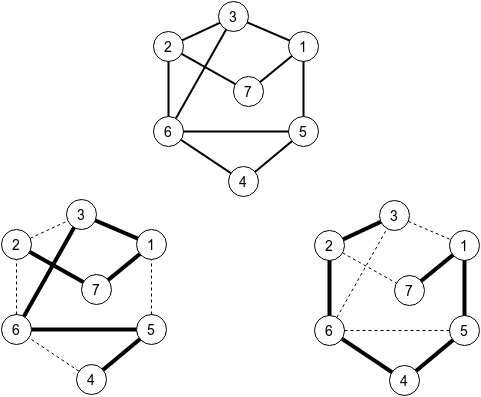
In the first sample test, there should be $ 7 $ cities and at most $ 11 $ roads. The provided sample solution generates $ 10 $ roads, as in the drawing. You can also see a simple path of length $ n $ between $ 2 $ and $ 4 $ , and a path between $ 7 $ and $ 3 $ .