CF643B Bear and Two Paths

Bearland 有 $n$ 个城市，编号为 $1$ 到 $n$。城市之间通过双向道路连接。每条道路连接两个不同的城市，没有两条道路连接相同的城市对。 有一次，Bear Limak 在城市 $a$，他想去城市 $b$。由于没有直接的道路，他决定进行一次长途旅行，恰好访问每个城市一次。形式化地说： - 城市 $a$ 和 $b$ 之间没有直接的道路。 - 存在一个包含 $n$ 个不同城市的序列 $v_1, v_2, ..., v_n$，满足 $v_1=a$，$v_n=b$，且对于所有 $1 \leq i < n$，$v_i$ 和 $v_{i+1}$ 之间有道路。 另外一天，同样的事情再次发生。Limak 想从城市 $c$ 到城市 $d$。同样地，他们之间没有直接道路，但存在一个包含 $n$ 个不同城市的序列 $u_1, u_2, ..., u_n$，满足 $u_1=c$，$u_n=d$，且对于所有 $1\leq i < n$，$u_i$ 和 $u_{i+1}$ 之间有道路。 此外，Limak 认为 Bearland 中最多只有 $k$ 条道路。他想知道自己记得对不对。 给定 $n$、$k$ 和四个互不相同的城市 $a$、$b$、$c$、$d$，你能否找到可能的路径（$v_1,\dots,v_n$ 和 $u_1,\dots,u_n$），使得所有给定条件都成立？请给出任意一种可行解，或者如果不可能则输出 $-1$。

输入的第一行包含两个整数 $n$ 和 $k$（$4\leq n\leq 1000$，$n-1\leq k\leq 2n-2$），表示城市数量以及道路数量的最大允许值。 第二行包含四个互不相同的整数 $a$、$b$、$c$、$d$（$1\leq a,b,c,d\leq n$）。

如果无法满足所有给定条件，请输出 $-1$。否则输出两行，每行描述一条路径。第一行应包含 $n$ 个不同的整数 $v_1,v_2,\dots,v_n$，其中 $v_1=a$，$v_n=b$。第二行应包含 $n$ 个不同的整数 $u_1,u_2,\dots,u_n$，其中 $u_1=c$，$u_n=d$。 两条路径最多生成 $2n-2$ 条道路：$(v_1,v_2),(v_2,v_3),\dots,(v_{n-1},v_n),(u_1,u_2),\dots,(u_{n-1},u_n)$。如果你的答案包含超过 $k$ 条不同的道路，或者不满足其他任何条件，则判为错误。注意，$(x,y)$ 与 $(y,x)$ 视为同一条道路。

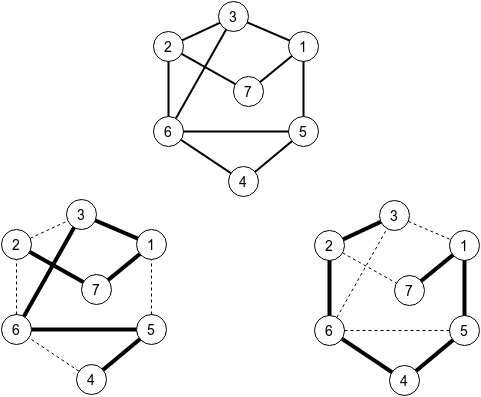
在第一个样例中，应该有 $7$ 个城市且最多有 $11$ 条道路。给出的样例解产生了 $10$ 条道路，如图所示。你也可以看到长度为 $n$ 的简单路径，分别连接 $2$ 和 $4$，以及 $7$ 和 $3$。  由 ChatGPT 5 翻译