CF643E Bear and Destroying Subtrees

Limak 是一只小灰熊。他未来会攻击 Deerland，但现在只能在角色扮演游戏中摧毁树木。Limak 从一棵只有一个节点的树开始。唯一的节点编号为 $1$，也是树的根节点。 有时，游戏会选择一棵子树，让 Limak 攻击它。当子树被攻击时，它的每一条边都会以 $0.5$ 的概率被摧毁（彼此独立）。然后，Limak 会得到一个惩罚——即子树受到攻击后高度的期望值。高度定义为子树根节点到任意节点路径中的最大边数。 你需要处理两种类型的操作： - $1~v$ 表示第一种操作。在节点 $v$ 下添加一个儿子新节点，新节点编号为当前未使用的最小编号（新节点的编号依次为 $2,3,\ldots$）。 - $2~v$ 表示第二种操作。假设子树以 $v$ 为根被攻击，Limak 得到的惩罚的期望值是多少？ 对于类型 $2$ 的操作，Limak 实际上并不会攻击子树，因此操作不会影响后续的操作。

输入的第一行是一个整数 $q$（$1 \le q \le 500000$），表示操作的数量。 接下来有 $q$ 行，每行包含两个整数 $type_i$ 和 $v_i$（$1 \le type_i \le 2$）。如果 $type_i=1$，则 $v_i$ 为本次要连接父节点的编号。如果 $type_i=2$，则请输出以 $v_i$ 为根的子树被攻击后的高度期望。 保证在第 $i$ 次操作前，编号为 $v_i$ 的节点已经存在。 保证至少有一次类型为 $2$ 的操作。

对于每一个类型为 $2$ 的操作，输出以 $v_i$ 为根的子树被攻击后惩罚的期望值，每个答案输出一个实数。如果你的绝对误差或相对误差不超过 $10^{-6}$，即可接受。 具体来说，假设你的答案为 $a$，标准答案为 $b$，则要求满足 $|a-b| \le 10^{-6} \max(1, |b|)$。

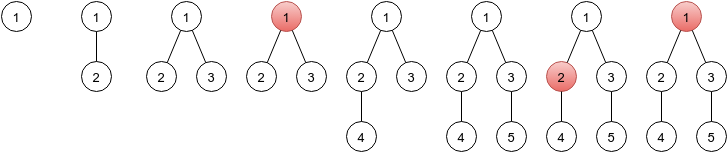
下面是第一个样例的结构图，红圈为类型 $2$ 的操作查询节点。  由 ChatGPT 5 翻译