CF645G Armistice Area Apportionment
Description
After a drawn-out mooclear arms race, Farmer John and the Mischievous Mess Makers have finally agreed to establish peace. They plan to divide the territory of Bovinia with a line passing through at least two of the $ n $ outposts scattered throughout the land. These outposts, remnants of the conflict, are located at the points $ (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n}) $ .
In order to find the optimal dividing line, Farmer John and Elsie have plotted a map of Bovinia on the coordinate plane. Farmer John's farm and the Mischievous Mess Makers' base are located at the points $ P=(a,0) $ and $ Q=(-a,0) $ , respectively. Because they seek a lasting peace, Farmer John and Elsie would like to minimize the maximum difference between the distances from any point on the line to $ P $ and $ Q $ .
Formally, define the difference of a line 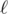 relative to two points $ P $ and $ Q $ as the smallest real number $ d $ so that for all points $ X $ on line 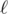, $ |PX-QX|
Input Format
The first line of the input contains two integers $ n $ and $ a $ ( $ 2
Output Format
Print a single real number—the difference of the optimal dividing line. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ .
Namely: let's assume that your answer is $ a $ , and the answer of the jury is $ b $ . The checker program will consider your answer correct, if 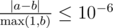.
Explanation/Hint
In the first sample case, the only possible line 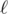 is $ y=x-1 $ . It can be shown that the point $ X $ which maximizes $ |PX-QX| $ is $ (13,12) $ , with , which is 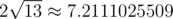.
In the second sample case, if we pick the points $ (0,1) $ and $ (0,-3) $ , we get  as $ x=0 $ . Because $ PX=QX $ on this line, the minimum possible difference is $ 0 $ .