CF650A Watchmen

Watchmen are in a danger and Doctor Manhattan together with his friend Daniel Dreiberg should warn them as soon as possible. There are $ n $ watchmen on a plane, the $ i $ -th watchman is located at point $ (x_{i},y_{i}) $ . They need to arrange a plan, but there are some difficulties on their way. As you know, Doctor Manhattan considers the distance between watchmen $ i $ and $ j $ to be $ |x_{i}-x_{j}|+|y_{i}-y_{j}| $ . Daniel, as an ordinary person, calculates the distance using the formula 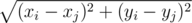. The success of the operation relies on the number of pairs $ (i,j) $ ( $ 1

The first line of the input contains the single integer $ n $ ( $ 1

Print the number of pairs of watchmen such that the distance between them calculated by Doctor Manhattan is equal to the distance calculated by Daniel.

In the first sample, the distance between watchman $ 1 $ and watchman $ 2 $ is equal to $ |1-7|+|1-5|=10 $ for Doctor Manhattan and 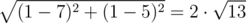 for Daniel. For pairs $ (1,1) $ , $ (1,5) $ and $ (7,5) $ , $ (1,5) $ Doctor Manhattan and Daniel will calculate the same distances.