CF650E Clockwork Bomb

我叫 James diGriz，是全银河系最聪明的窃贼和寻宝猎人。关于我的冒险经历有专门的书籍和歌曲，尽管这次你把我抓了个正着。 我能避开摄像头，智胜所有守卫，穿越重重陷阱。但当我终于到达藏宝箱并打开它时，却意外启动了发条炸弹！幸运的是，我以前见过这种炸弹，并且知道通过在炸弹控制面板上以特定方式用导线连接触点，可以让发条机关停止。 我看到有 $n$ 个触点，通过 $n-1$ 根导线连接。触点编号为 $1$ 到 $n$ 的整数。炸弹有一个安全机制，保证下述条件：如果存在 $k \geq 2$ 个触点 $c_1,c_2,\ldots,c_k$ 形成一个回路，也就是说，存在 $k$ 根不同的导线，连接 $c_1$ 与 $c_2$、$c_2$ 与 $c_3$、……、$c_k$ 与 $c_1$，那么炸弹会立即爆炸，我的故事也将在这里结束。特别地，如果两个触点被多根导线连接，则会形成长度为 $2$ 的回路。同样不允许导线连接同一个触点自身。 另一方面，如果我断开多于一根导线（也就是说，某一时刻方案中最多只有 $n-2$ 根导线），另一道安全检查就会失效，炸弹同样会爆炸。因此，我唯一能做的就是把某一根导线从当前位置拔下来并插到另一个地方，同时保证不会出现回路。 我已经知道该如何重新连接导线以让发条机关停止。但我的时间不多了！帮我活着逃出去：找出一系列操作，每次操作包括拔掉某一根导线并插到新位置，从而拆除炸弹。

第一行输入一个整数 $n$（$2 \leq n \leq 500000$），表示触点的个数。 接下来的 $n-1$ 行，每行两个整数 $x_i$ 和 $y_i$（$1 \leq x_i, y_i \leq n$，$x_i \neq y_i$），表示第 $i$ 根导线目前连接的触点编号。 紧接着的 $n-1$ 行，以同样的格式描述目标方案。 保证起始方案与目标方案都正确（即没有回路、也没有导线连接自身）。

第一行输出一个整数 $k$（$k \geq 0$）——需要进行的最少拔插导线操作次数。 接下来 $k$ 行，每行四个整数 $a_i, b_i, c_i, d_i$，表示第 $i$ 次操作为：拔掉连接 $a_i$ 和 $b_i$ 的导线，并插到连接 $c_i$ 和 $d_i$ 的位置。显然，在每次操作前，$a_i$ 和 $b_i$ 应该是当前方案中相连的一对触点。 如果不存在可行的操作序列使得初始方案变为目标方案，则输出 -1。

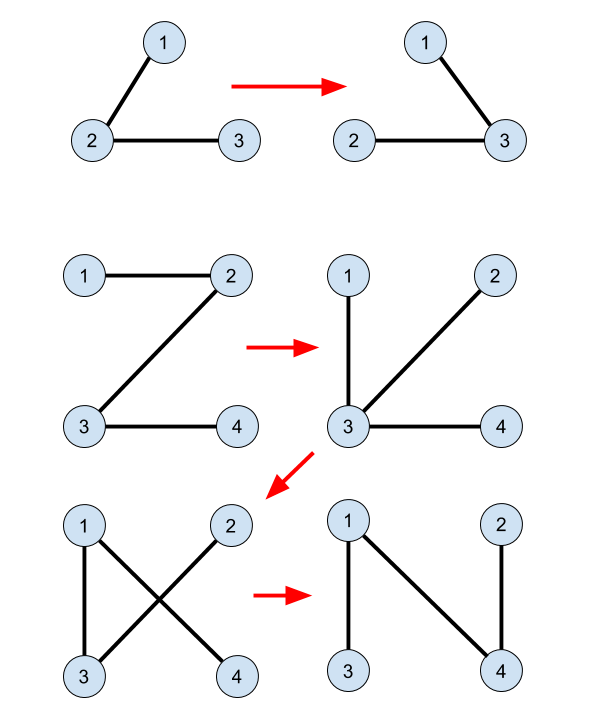
下面的图片可以帮助理解样例测试中的说明：  由 ChatGPT 5 翻译