CF653D Delivery Bears

Niwel 是一只可爱的小金熊。众所周知，熊通常生活在森林里，但 Niwel 厌倦了看见满眼的树木，于是决定搬到城市里去。 在城市里，Niwel 接手了一份管理熊队送货的工作。他居住的城市可以被表示为一个有向图，包含 $n$ 个节点和 $m$ 条边，每条边都有一个承重容量。一次送货由熊们从节点 $1$ 运输货物到节点 $n$，每只熊都可以选择一条简单路径（不重复边和节点）来完成运输。通过某条边的货物总重量不能超过该边的承重容量。 Niwel 手上正好有 $x$ 只熊。为保证公平，所有熊不能休息，而且每只熊所搬运的货物重量必须完全相同。但每只熊可以选择不同的路径。 Niwel 想知道，最多能送多少货物？即这些熊能运送的总货物重量最大值是多少。

第一行包含三个整数 $n$、$m$ 和 $x$（$2 \leq n \leq 50$，$1 \leq m \leq 500$，$1 \leq x \leq 100000$），分别表示节点数量、有向边数量和熊的数量。 接下来的 $m$ 行，每行包含三个整数 $a_i$、$b_i$ 和 $c_i$（$1 \leq a_i, b_i \leq n$，$a_i \neq b_i$，$1 \leq c_i \leq 1000000$）。表示一条从节点 $a_i$ 指向节点 $b_i$ 的有向边，该边的承重上限为 $c_i$。图中没有自环，也不存在多重边。更正式地说，对于任意 $i \neq j$，都有 $a_i \neq a_j$ 或 $b_i \neq b_j$。保证至少存在一条从点 $1$ 到点 $n$ 的路径。

输出一个实数，表示 Niwel 最多可以运送的总货物重量（即所有熊携带货物的总和），要求恰好使用 $x$ 只熊。你的答案只要绝对或相对误差不超过 $10^{-6}$ 即被认为是正确的。 也就是说，假如你的答案为 $a$，标准答案为 $b$，那么当 \[ \frac{|a-b|}{\max(1,|b|)} \leq 10^{-6} \] 时，将被视为正确。

在第一个样例中，Niwel 有三只熊。两只熊可以选择路径 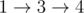，而另一只熊可以走路径 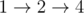。即使最后一只熊能够单独搬运 1 单位的货物，为了公平，它也只能搬运 $0.5$ 单位重量。因此总共可以搬运 $1.5$ 单位货物。注意，虽然 Niwel 仅用两只熊可以搬运更多货物，但今天必须恰好用三只熊。 由 ChatGPT 5 翻译