CF659D Bicycle Race

玛利亚参加了一场自行车比赛。 比赛赛道沿着卢塞恩湖的湖岸线铺设，完全按照湖岸线的轮廓。众所周知，湖岸线仅由朝向正北、正南、正东或正西的直线段组成。 设定一个坐标系，将 $Ox$ 轴指向从西到东，$Oy$ 轴指向从南到北。比赛的起点选在赛道上最南端的点（若有多个，则选最西边的那个）。参赛者从北方出发。赛道上的每一段直线的行驶方向只可能是四个基本方向之一（北、南、东或西），只有在转弯处才会改变方向。参赛者绝不会掉头，也就是说不会从北转南或从东转西（或反向）行驶。 玛利亚年纪尚小，对某些弯道还把握不准。具体来说，如果在某个弯道处，由于操作失误或转弯不及时而驶出赛道，她就会直接掉进湖里。换句话说，玛利亚认为若忽略了某个弯道就会立即掉进湖里，则此弯道是“危险弯道”。 请帮助玛利亚为比赛做好准备——确定赛道上危险弯道的数量。

输入的第一行包含一个整数 $n$（$4 \leq n \leq 1000$），表示赛道的直线段数。 接下来的 $n+1$ 行中，每行包含一对整数 $(x_i, y_i)$（$-10000 \leq x_i, y_i \leq 10000$）。第一对坐标是比赛的起点。第 $i$ 段直线赛道起点为 $(x_i, y_i)$，终点为 $(x_{i+1}, y_{i+1})$。 保证条件如下： - 第一段赛道指向正北； - 最南端（若有多个则最西端）的点位于第一行； - 最后一个点与第一个点重合（即起点和终点相同）； - 任意两段赛道没有公共点（相邻的除外，相邻只共享一个点）； - 没有两点（除起点和终点）坐标相同； - 相邻两段赛道不会朝同一方向，也不会反向。

输出一个整数，表示赛道上危险弯道的数量。

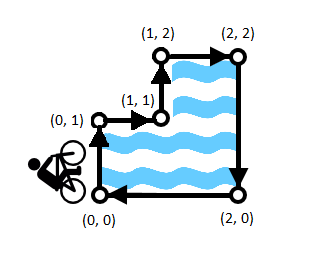
第一个样例对应下图：  图中只有在点 $(1,1)$ 处的弯道，玛利亚可能一冲就掉进湖里，所以答案是 $1$。 由 ChatGPT 5 翻译