CF659E New Reform

题目描述

有 $n$ 个城市，$m$ 条双向道路，没有一个城市存在自己到自己的道路，两个不同的城市间，最多有一条道路，也不能保证能从一个城市到达任意一个其他城市。现在需要对每一条道路定向，使之成为单向道路，当然需要尽可能少地产生孤立的城市。当其他所有城市都不能到达某个城市，则称这个城市为孤立城市。要求出最少的孤立城市的个数。

输入格式

无

输出格式

无

说明/提示

In the first sample the following road orientation is allowed: 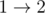![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/bbf0ca4cbc925b1d673ae3b61e28811a0ccacf51.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/851f40f264708d94590f3171217fe3d9e053dcee.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/a78766420998fc575b76dcce0681c08c42ea944a.png). The second sample: 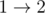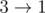![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/bbf0ca4cbc925b1d673ae3b61e28811a0ccacf51.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/43ec097315a08660c95bbf7f709c76c8ce606dd6.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/f1138b32236a89525fad2b8c02b9cbfbd546dfad.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/251db88dae63817bf4f821cd1c34afb5e431b414.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/a78766420998fc575b76dcce0681c08c42ea944a.png). The third sample: 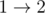![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/bbf0ca4cbc925b1d673ae3b61e28811a0ccacf51.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/f1138b32236a89525fad2b8c02b9cbfbd546dfad.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/2463f630c8ccc890fae1e6f138ebd6eef6182a64.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/e28d0fe9fd144c4ace5d77ff789151d059a9a237.png), ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF659E/8a5be1e7dc973906ccbd327695b9e6d157596058.png).