CF659G Fence Divercity

很久以前，Vasily 在他的乡间别墅建造了一道漂亮的栅栏。Vasily 认为栅栏是好的，如果它由 $n$ 块宽度为 1 厘米的竖直木板连续紧密相连组成，每一块的高度（单位：厘米）都是一个正整数。房主记得，从左到右第 $i$ 块木板的高度是 $h_{i}$。 今天，Vasily 决定改变他建好的栅栏的设计，方法是在顶端切掉一段连续的部分，使得剩下的栅栏依然是好的。被切掉的部分仅包含各块木板的上部，相邻部分必须连接（也就是说在被切掉之前它们有非零长度共同边）。 作为 Vasily 好奇的邻居，你想计算出满足上述要求、切掉恰好一段连通部分的方法数。如果对于剩余的栅栏，存在某个 $i$ 使得第 $i$ 块木板的高度不同，则视为两种不同的切割方式。 由于 Vasily 的栅栏可能非常高且很长，输出所需的切割方法数对 $1000000007$ $(10^9+7)$ 取余的结果。

第一行包含整数 $n$（$1 \leq n \leq 1000000$）——Vasily 的栅栏中木板的数量。 第二行包含 $n$ 个用空格分隔的数 $h_1, h_2, ..., h_n$（$1 \leq h_i \leq 10^9$），其中 $h_i$ 表示从左到右第 $i$ 块木板的高度。

输出一个整数，表示切取恰好一段连通部分的方案数，再对 $1000000007$ 取余。

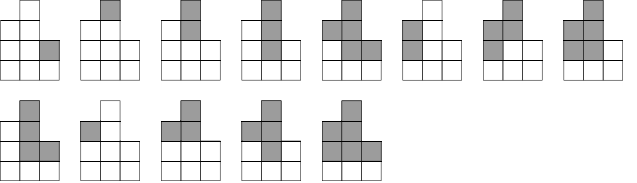
在第一个样例中的栅栏，不可能切取恰好一段，使得剩余的栅栏依旧是好的。 第二个样例的所有可能操作如下（图中灰色部分为被切掉的部分）：  由 ChatGPT 5 翻译