CF660F Bear and Bowling 4

Limak is an old brown bear. He often goes bowling with his friends. Today he feels really good and tries to beat his own record! For rolling a ball one gets a score — an integer (maybe negative) number of points. Score for the $ i $ -th roll is multiplied by $ i $ and scores are summed up. So, for $ k $ rolls with scores $ s_{1},s_{2},...,s_{k} $ , the total score is 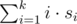. The total score is $ 0 $ if there were no rolls. Limak made $ n $ rolls and got score $ a_{i} $ for the $ i $ -th of them. He wants to maximize his total score and he came up with an interesting idea. He can say that some first rolls were only a warm-up, and that he wasn't focused during the last rolls. More formally, he can cancel any prefix and any suffix of the sequence $ a_{1},a_{2},...,a_{n} $ . It is allowed to cancel all rolls, or to cancel none of them. The total score is calculated as if there were only non-canceled rolls. So, the first non-canceled roll has score multiplied by $ 1 $ , the second one has score multiplied by $ 2 $ , and so on, till the last non-canceled roll. What maximum total score can Limak get?

The first line contains a single integer $ n $ ( $ 1

Print the maximum possible total score after cancelling rolls.

In the first sample test, Limak should cancel the first two rolls, and one last roll. He will be left with rolls $ 1,-3,7 $ what gives him the total score $ 1·1+2·(-3)+3·7=1-6+21=16 $ .