CF666B World Tour

著名雕塑家 Cicasso 要去进行一次“世界巡回之旅”！ 不过，这其实并不是一场真正意义上的全球巡演。毕竟，并不是每个人都有机会亲眼见到雕塑家的作品，不是吗？要不然，展览就不独特了。所以，Cicasso 的世界巡回展将全部只在他的祖国 Berland 举行。 Cicasso 对自己的工作极为投入，他希望能尽量少被打扰。因此，这次他只会访问 4 个城市。这些城市必须各不相同，以免别人觉得他有“偏爱”。当然，为了节省开销，他会选择各城市间的最短路径。但如你所料，Cicasso 有点怪。他虽然不爱办展，却热衷于环游祖国、欣赏风景。所以，他希望他旅途的总距离尽可能长。不过，Cicasso 不擅长规划路线，所以他向你求助。 Berland 有 $n$ 个城市和 $m$ 条单向公路。你需要选择 4 个不同的城市让 Cicasso 依次访问，并确定访问顺序。使得按照你给定的顺序，从第一个城市出发，按次序访问每对城市时都走最短路径，总旅程长度最大。 注意，中间路线可以经过这次分配参观的城市，也可以多次经过同一个城市。例如，下图路线的顺序为 $[1,5,2,4]$，用下划线表示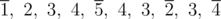：。 请注意，Berland 是一个高科技国家。利用纳米技术，所有公路长度都统一了。因此，人们很少用普通汽车出行，有的城市对另一城市甚至压根无法开车到达。不过 Cicasso 非常保守，他不能离开汽车出行。请你选择一组城市，让雕塑家能够仅靠汽车完成整个旅程。保证一定可以达成这种路线。

第一行输入两个整数 $n$ 和 $m$（$4 \leq n \leq 3000, 3 \leq m \leq 5000$），分别表示 Berland 的城市数量和单向公路数量。 接下来的 $m$ 行，每行包含两个整数 $u_{i}, v_{i}$（$1 \leq u_{i}, v_{i} \leq n$），表示一条从城市 $u_{i}$ 到城市 $v_{i}$ 的单向公路。注意 $u_{i}$ 和 $v_{i}$ 不必不同。同一对城市间可能有多条单向公路。

输出 4 个整数，依次表示 Cicasso 按最优路线访问的城市序号。若有多解，输出任意一组均可。

设 $d(x,y)$ 为城市 $x$ 到城市 $y$ 间的最短距离。那么样例中 $d(2,1)=3$，$d(1,8)=7$，$d(8,7)=3$，总路程为 $13$。 由 ChatGPT 5 翻译