CF676B Pyramid of Glasses
题目描述
Mary 刚刚从一所著名大学毕业,现在正在参加庆祝派对。学生们总喜欢憧憬美好生活,于是他们用香槟杯搭建了一个小金字塔。该金字塔的高度为 $n$。金字塔的最顶层只有 $1$ 个酒杯,第二层(自上而下计)有 $2$ 个酒杯,第三层有 $3$ 个酒杯,依此类推,最底层共有 $n$ 个酒杯。
Vlad 在电影中多次见过香槟从金字塔顶端流向下方,所有酒杯都能同时被注满的场景。因此,他拿起一瓶香槟,开始向金字塔顶端的酒杯倒酒。
每秒钟,Vlad 向顶端的酒杯倒入正好相当于一个酒杯容量的香槟。如果某个酒杯已满,但仍继续被倒入香槟,溢出的香槟会平均分流到其下方的两个酒杯。如果溢出的酒杯位于金字塔的底层,则溢出的香槟将直接流到桌子上。为简化问题,假设香槟在金字塔中的流动是瞬时完成的。Vlad 想知道,如果他共倒 $t$ 秒香槟,在停止倒酒时有多少个酒杯是刚好被填满的。
下图展示了一个三层金字塔。
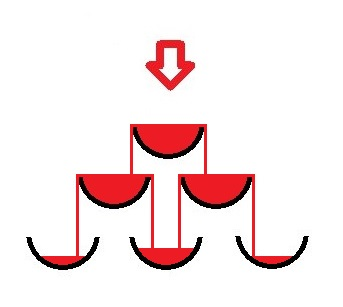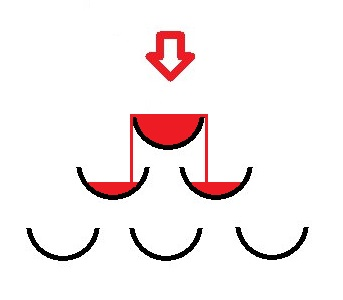
输入格式
输入仅一行,包含两个整数 $n$ 和 $t$($1 \leq n \leq 10,\,0 \leq t \leq 10000$),分别表示金字塔的高度和 Vlad 倒香槟的秒数。
输出格式
输出一个整数,表示在倒酒结束后,刚好被填满的酒杯数量。
说明/提示
在第一个样例中,经过 $5$ 秒后,完全装满的酒杯有:顶层的酒杯、第二层的两个酒杯以及底层中间的酒杯。底层左右两侧的酒杯各有一半是空的。
由 ChatGPT 5 翻译