CF67E Save the City!

在 `Aalam-Aara`（意为大地之光）镇，以前没有犯罪，没有罪犯。但随着时间的推移，罪恶开始蔓延到曾经正义的人们的心中。为了解决这个问题，一些长老发现，只要将人口中腐败的部分远离未腐败的部分，犯罪就可以停止。所以，他们正试图建立一个可以关押腐败人民的大院。为确保不法分子逃出大院，需要设置瞭望塔，以便对其进行监视。 由于 `Aalam-Aara` 的人民不是很富有，他们遇到了一个来自某个富裕城镇的商人，他同意将一块地块卖给他们，该地块已经有一条直线围栏 $AB$，沿围栏设置了几个点。可以建瞭望塔。你的任务是帮助他们找出栅栏上可以架设塔楼的点数，以便从那里监视所有罪犯。只能设置一个瞭望塔。如果从瞭望塔到罪犯的视线没有在他和塔之间的任何点穿过情节边缘，即如下图 $1$ 所示，点 $X$、$Y$、$C$ 和 $A$ 是可以从瞭望塔观察到的从 $B$ 点可见，但 $E$ 和 $D$ 点不可见。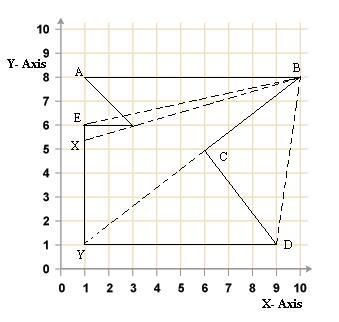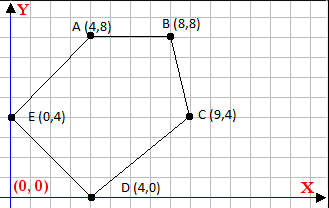 \ 　　　　　　　　　　　图$1$ \ 　　　　　　　　　　　图$2$ 假设地块为多边形，坐标轴设置为围栏$AB$平行于$x$轴，可以设置瞭望塔的点是直线上的整数点。 例如，在给定的图 $2$ 中，瞭望塔可以设置在 $AB$ 上的五个整数点中的任何一个，即 $(4,8)$、$(5,8)$、$(6,8)$、$(7,8)$ 或 $(8,8)$. 您可以假设没有三个连续的点共线，并且除 $A$ 和 $B$ 之外的所有角点都位于围栏 $AB$ 的同一侧。 给定的多边形不包含自相交。

测试用例的第一行将包含顶点数 $n$ $(3 \le n \le 100)$。 接下来的 $n$ 行将包含按多边形顺时针顺序排列的顶点坐标。第 $i$ 行是整数 $x_i$ 和 $y_i$ $(0 \le x_i, y_i \le 10^6)$。 围栏$AB$的端点是前两个点 $(x_1,y_1)$ 和 $(x_2,y_2)$。

输出可以设置瞭望塔的点数个数。

图 $2$ 显示了第一个测试用例。 图中的所有点都可以从围栏 $AB$ 上的任何点看到。 因为， $AB$ 有 $5$ 个整数坐标，所以答案是 $5$ 。 对于情况二，围栏 $CD$ 和 $DE$ 不完全可见，因此答案为 $0$ 。