CF682C Alyona and the Tree
题目描述
给你一棵树,边与节点都有权值,根节点为 $1$,现不停删除叶子节点形成新树,问最少删掉几个点,能使得最后剩下的树内,$\forall v$ 与其子树内 $\forall u$ 间边权的和小于等于点 $u$ 权值。
输入格式
第一行,节点个数 $n(1 \leq n \leq 10^5)$。
第二行,$n$ 个整数——各节点的权值 $a_i(1\leq a_i \leq 10^9)$。
接下来的 $n-1$ 行,每行两个整数 $p_i$ 与 $c_i(1 \leq p_i \leq n,-10^9 \leq c_i \leq 10^9)$,分别表示编号为 $i+1$ 的节点的父节点以及该边的边权。
输出格式
一个整数,最少需要删除的点的个数。
说明/提示
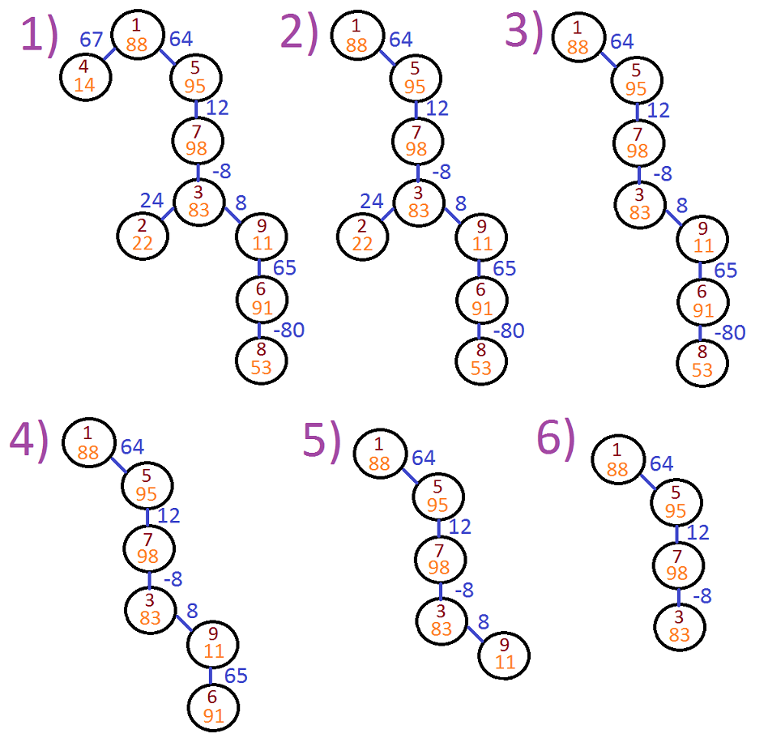
The following image represents possible process of removing leaves from the tree: