CF685B Kay and Snowflake
题目描述
当魔镜碎片击中凯的眼睛后,他对玫瑰的美再也不感兴趣了。现在他喜欢观察雪花。
有一天,他发现了一片巨大的雪花,这片雪花的结构是一棵有 $n$ 个结点的树(即连通无环图)。树的根节点编号为 $1$。凯对这棵树的结构非常感兴趣。
经过一些研究,他对这棵树产生了 $q$ 个问题。第 $i$ 个问题请求你找到以第 $v_i$ 号节点为根的子树的重心。
一个节点的子树是指由该节点及其所有后代(无论是直接的还是间接的)组成的部分。换句话说,节点 $v$ 的子树包含所有满足从节点 $u$ 到根节点的路径经过 $v$ 的结点。
一棵树(或子树)的重心是指这样一个节点:如果我们删除它,所得到的最大连通块的大小不超过原树(或子树)大小的一半。
输入格式
输入的第一行包含两个整数 $n$ 和 $q$($2\leq n\leq 300000$,$1\leq q\leq 300000$),分别表示初始树的结点数和询问的数量。
第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$($1\leq p_i\leq n$),表示编号为 $2$ 到 $n$ 的节点的父节点编号。节点 $1$ 是树的根节点。保证 $p_i$ 所描述的是一棵合法的树。
接下来的 $q$ 行,每行一个整数 $v_i$($1\leq v_i\leq n$),表示一个问题 —— 以 $v_i$ 为根的子树,要求你找出它的重心。
输出格式
对于每个查询,输出对应子树重心的编号。如果存在多个满足条件的节点,输出其中任意一个即可。保证每个子树至少有一个重心。
说明/提示
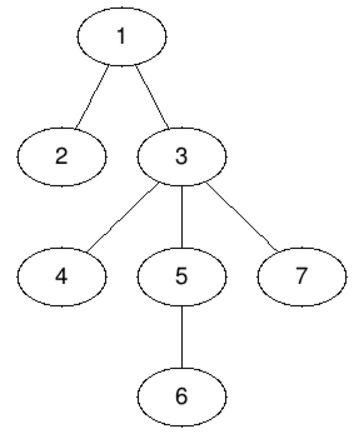
如下图所示,第一组询问要求整棵树的重心——即节点 $3$。如果删除节点 $3$,树被分为四个连通块,其中两个大小为 $1$,两个大小为 $2$。
编号为 $2$ 的节点的子树只包含它自己,因此答案是 $2$。
编号为 $3$ 的节点自己的子树的重心是 $3$。
编号为 $5$ 的节点的子树的重心可以是 $5$ 或 $6$,两者都为正确答案。
由 ChatGPT 5 翻译