CF685B Kay and Snowflake

当魔镜碎片击中凯的眼睛后，他对玫瑰的美再也不感兴趣了。现在他喜欢观察雪花。 有一天，他发现了一片巨大的雪花，这片雪花的结构是一棵有 $n$ 个结点的树（即连通无环图）。树的根节点编号为 $1$。凯对这棵树的结构非常感兴趣。 经过一些研究，他对这棵树产生了 $q$ 个问题。第 $i$ 个问题请求你找到以第 $v_i$ 号节点为根的子树的重心。 一个节点的子树是指由该节点及其所有后代（无论是直接的还是间接的）组成的部分。换句话说，节点 $v$ 的子树包含所有满足从节点 $u$ 到根节点的路径经过 $v$ 的结点。 一棵树（或子树）的重心是指这样一个节点：如果我们删除它，所得到的最大连通块的大小不超过原树（或子树）大小的一半。

输入的第一行包含两个整数 $n$ 和 $q$（$2\leq n\leq 300000$，$1\leq q\leq 300000$），分别表示初始树的结点数和询问的数量。 第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$（$1\leq p_i\leq n$），表示编号为 $2$ 到 $n$ 的节点的父节点编号。节点 $1$ 是树的根节点。保证 $p_i$ 所描述的是一棵合法的树。 接下来的 $q$ 行，每行一个整数 $v_i$（$1\leq v_i\leq n$），表示一个问题 —— 以 $v_i$ 为根的子树，要求你找出它的重心。

对于每个查询，输出对应子树重心的编号。如果存在多个满足条件的节点，输出其中任意一个即可。保证每个子树至少有一个重心。

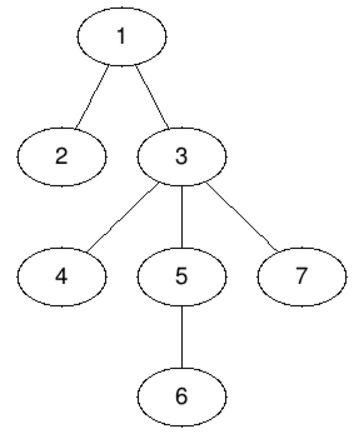
如下图所示，第一组询问要求整棵树的重心——即节点 $3$。如果删除节点 $3$，树被分为四个连通块，其中两个大小为 $1$，两个大小为 $2$。 编号为 $2$ 的节点的子树只包含它自己，因此答案是 $2$。 编号为 $3$ 的节点自己的子树的重心是 $3$。 编号为 $5$ 的节点的子树的重心可以是 $5$ 或 $6$，两者都为正确答案。  由 ChatGPT 5 翻译