CF687B Remainders Game

Today Pari and Arya are playing a game called Remainders. Pari chooses two positive integer $ x $ and $ k $ , and tells Arya $ k $ but not $ x $ . Arya have to find the value 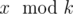. There are $ n $ ancient numbers $ c_{1},c_{2},...,c_{n} $ and Pari has to tell Arya 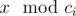 if Arya wants. Given $ k $ and the ancient values, tell us if Arya has a winning strategy independent of value of $ x $ or not. Formally, is it true that Arya can understand the value 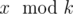 for any positive integer $ x $ ? Note, that 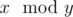 means the remainder of $ x $ after dividing it by $ y $ .

The first line of the input contains two integers $ n $ and $ k $ ( $ 1

Print "Yes" (without quotes) if Arya has a winning strategy independent of value of $ x $ , or "No" (without quotes) otherwise.

In the first sample, Arya can understand 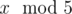 because $ 5 $ is one of the ancient numbers. In the second sample, Arya can't be sure what 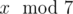 is. For example $ 1 $ and $ 7 $ have the same remainders after dividing by $ 2 $ and $ 3 $ , but they differ in remainders after dividing by $ 7 $ .