CF696A Lorenzo Von Matterhorn
题目描述
Barney 住在纽约市。纽约有无限多个路口,这些路口用正整数从 $1$ 开始编号。对于每个正整数 $i$,存在一条双向道路连接路口 $i$ 到 $2i$,还有一条双向道路连接 $i$ 到 $2i+1$。你可以清楚地看到,任意两个路口之间存在唯一的一条最短路径。

起初,任何人都可以免费通过任意道路。但由于 SlapsGiving 即将来临,接下来会有 $q$ 个连续事件。事件有两种类型:
1. 政府制定新规定。该规定由整数 $v$、$u$ 和 $w$ 表示。该操作的结果是,使得从 $u$ 到 $v$ 的最短路径上的所有道路的通行费用增加 $w$ 美元。
2. Barney 从某个路口 $v$ 出发,前往路口 $u$ 去找一个他想要拥抱的女孩(用他的假名 Lorenzo Von Matterhorn)。他总是选择从 $v$ 到 $u$ 间访问最少路口(道路)的唯一一条最短路径。
政府需要你来进行计算。每当 Barney 去找女孩时,你需要告诉政府他应当支付多少路费(即他经过的所有道路的通行费用之和)。
输入格式
输入的第一行包含一个整数 $q$($1 \leq q \leq 1000$)。
接下来的 $q$ 行按照时间顺序给出事件信息。每个事件描述形式如下:
- 如果是政府增加路费的事件,格式为 $1\ v\ u\ w$;
- 如果是 Barney 前往某个路口的事件,格式为 $2\ v\ u$。
这里 $1 \leq v, u \leq 10^{18}$,$v \ne u$,$1 \leq w \leq 10^9$。
输出格式
对于每一次 Barney 前往找女孩的事件,输出他在该事件中需要支付的路费总和,每行输出一个答案。按事件发生的时间顺序输出。
说明/提示
在样例测试中,使用到的路口如下:
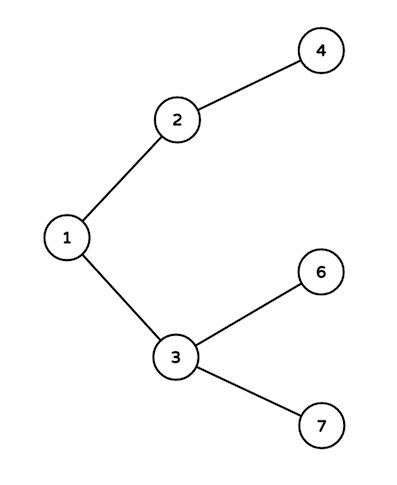
1. 路径上的路口为 $3$,$1$,$2$ 和 $4$。
2. 路径上的路口为 $4$,$2$ 和 $1$。
3. 路径上的路口仅为 $3$ 和 $6$。
4. 路径上的路口为 $4$,$2$,$1$ 和 $3$。路径上道路的通行费用依次为 $32$,$32$ 和 $30$,所以答案为 $32+32+30=94$。
5. 路径上的路口为 $6$,$3$ 和 $1$。
6. 路径上的路口为 $3$ 和 $7$。两者之间道路通行费用为 $0$。
7. 路径上的路口为 $2$ 和 $4$。两者之间道路的通行费用为 $32$(在第一次事件中增加了 $30$,在第二次事件中增加了 $2$)。
由 ChatGPT 5 翻译