CF698B Fix a Tree

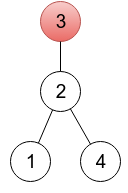
对于下图中的树，  可以用**数组**表示为 $[2,3,3,2]$。这种可以表示树的数组（即**有效**）需要符合以下条件： 1. 有且只有一个索引 $r$，符合 $p_r=r$。其中顶点 $r$ 是树的根。 2. 对于所有剩下的 $n-1$ 个顶点 $i$ 一定要有在 $i$ 和 $p_i$ 之间的边。 比如 数列 $(1,2,2)$、$(2,3,1)$ 和 $(2,1,3)$ 都是因为**根**的数目而导致不**有效**。 现在给你一个**数组** $a_1,a_2,\cdots ,a_n$，**不一定**是**有效**的。你需要对数组里面的值，通过**最小次数**的**更改**，使得这个数组**有效**。 并输出**最小更改次数**和一个通过最小更改次数而更改成功的**有效数组**。 如果有多种解，只需说出任何一组。

第一行是一个整数 $n\ (2\le n \le 200000)$----树的顶点个数。 第二行包含 $n$ 个整数 $a_1,a_2,\cdots ,a_n\ (1\le a_i\le n)$。

第一行一个整数，**最小更改次数**。 第二行输出任意一个通过**最小更改次数**而更改成功的有效数组。

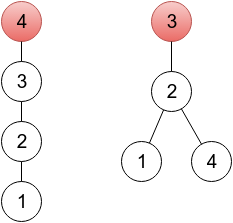
- 第一个样例只需要改一个就好啦！第一个样例输出是一个扎根于顶点 $4$ 的树（因为 $p_4=4$），你可以在下面的图中看到。另一个正确的答案应该是数列 $2,3,3,2$，扎根在顶点 $3$，也可以在下面的图中看到。两个图中顶点将用红色标出。  - 第二个样例中，给出的数列已经是有效的了。