CF698F Coprime Permutation

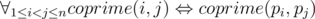
当且仅当两个正整数没有大于 $1$ 的公约数时，这两个数互质。 有只熊不想告诉 Radewoosh 怎么解决某道算法题。因此，Radewoosh 打算闯进这只熊藏有解答的保险箱中。为了通过那道门，他需要输入 $1$ 到 $n$ 的一个排列。门只有在输入的排列 $p_{1},p_{2},...,p_{n}$ 满足如下条件时才会打开：  换句话说，当且仅当两个下标互质时，对应的两个数也互质。 排列中的部分值可能已经被确定。Radewoosh 要有多少种不同的方式填补剩下的空位，使得门能够打开？请将答案对 $10^{9}+7$ 取模。

第一行输入一个整数 $n$，满足 $2 \leq n \leq 1000000$。 第二行输入 $n$ 个整数 $p_{1},p_{2},...,p_{n}$，其中 $0 \leq p_{i} \leq n$。如果 $p_{i}=0$ 表示该位置有空，需要填补；如果 $p_{i} \geq 1$，表示该位置的值已经确定。 保证如果 $i \neq j$ 且 $p_{i},p_{j} \geq 1$，则 $p_{i} \neq p_{j}$。

输出能够填补空位并打开门的方案数，对 $1000000007$ 取模。

在第一个样例中，4 个元素都未被固定。共有 4 个满足条件的排列：(1,2,3,4)、(1,4,3,2)、(3,2,1,4)、(3,4,1,2)。 在第二个样例中，$p_{3}=1$ 且 $p_{4}=2$ 已被固定。满足条件的排列有两种：(3,4,1,2,5)、(5,4,1,2,3)。 由 ChatGPT 5 翻译