CF702E Analysis of Pathes in Functional Graph

You are given a functional graph. It is a directed graph, in which from each vertex goes exactly one arc. The vertices are numerated from $0$ to $ n-1 $. Graph is given as the array $ f_{0},f_{1},\dots,f_{n-1} $, where $ f_{i} $ — the number of vertex to which goes the only arc from the vertex $ i $. Besides you are given array with weights of the arcs $ w_{0},w_{1},\dots,w_{n-1} $, where $ w_{i} $ — the arc weight from $ i $ to $ f_{i} $.  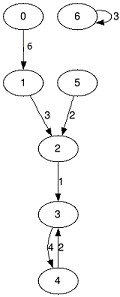The graph from the first sample test.Also you are given the integer $ k $ (the length of the path) and you need to find for each vertex two numbers $ s_{i} $ and $ m_{i} $, where: - $ s_{i} $ — the sum of the weights of all arcs of the path with length equals to $ k $ which starts from the vertex $ i $; - $ m_{i} $ — the minimal weight from all arcs on the path with length $ k $ which starts from the vertex $ i $. The length of the path is the number of arcs on this path.

The first line contains two integers $ n,k \ ( 1\le n \le10^{5},1\le k\le10^{10}) $. The second line contains the sequence $ f_{0},f_{1},\dots,f_{n-1}\ ( 0\le f_{i}

Print $ n $ lines, the pair of integers $ s_{i},m_{i} $ in each line.