CF703C Chris and Road

当 Mishka 正在享受她的旅行时…… Chris 是一只小棕熊。没人知道他是什么时候、在哪里遇见 Mishka 的，但他们已经一起很长时间了（这次旅行除外）。当然，最好的朋友也很重要。John 是 Chris 最好的朋友。 有一天，Chris 和 John 一起散步时，John 给了 Chris 这样一道题： 在宽度为 $w$ 的无限水平道路上（道路的边界是直线 $y=0$ 和 $y=w$），有一辆巴士正在移动，巴士由一个有 $n$ 个顶点的凸多边形表示。巴士以速度 $v$ 沿 $Ox$ 轴负方向（即 $x$ 坐标递减方向）匀速直线移动，因此，巴士上每一个点的 $x$ 坐标都会随时间减少。形式化地说，经过时间 $t$ 后，每个顶点的 $x$ 坐标都会减少 $vt$。 在点 $(0,0)$ 有一个行人，他只能沿垂直于道路的斑马线行走。斑马线是一条连接 $(0,0)$ 和 $(0,w)$ 的线段，行人可以以不超过 $u$ 的任意速度沿直线 $Oy$ 方向双向移动，但不能离开道路边界。行人可以瞬间改变自己的速度，例如可以瞬间停止。 为便于理解，请参见样例说明图。 如果在任意时刻，行人所处的点严格在巴士凸多边形内部，则认为他被巴士撞到了（如果点落在多边形的顶点或边上，则不算被撞）。 现在给出时刻 $0$ 时巴士的位置，请帮助 Chris 计算行人横穿道路从 $(0,0)$ 到达 $(0,w)$ 且不被巴士撞到所需的最短时间。

第一行包含四个整数 $n$、$w$、$v$、$u$（$3 \leq n \leq 10000$，$1 \leq w \leq 10^9$，$1 \leq v, u \leq 1000$）——巴士凸多边形的顶点数量、道路宽度、巴士速度和行人速度。 接下来的 $n$ 行，每行两个整数 $x_i$ 和 $y_i$（$-10^9 \leq x_i \leq 10^9$，$0 \leq y_i \leq w$），表示按照逆时针顺序给出的每个多边形顶点的坐标。保证给定的是一个非退化的凸多边形。

输出一个实数 $t$，表示行人横穿道路且不被巴士撞到所需的最短时间。如果输出的答案与真实答案的绝对误差或相对误差不超过 $10^{-6}$ ，则认为是正确的。

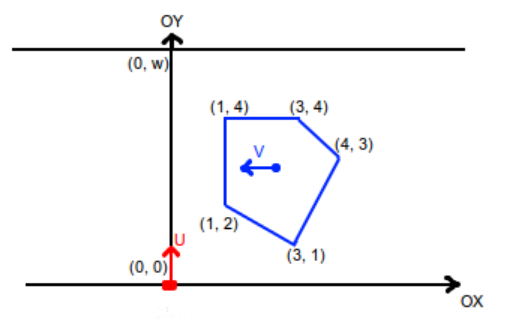
下图描述了第一个样例中的初始位置：  由 ChatGPT 5 翻译