CF703C Chris and Road

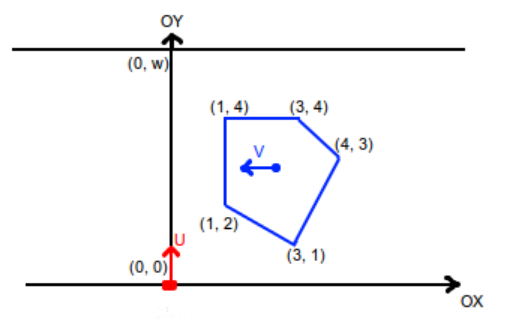
And while Mishka is enjoying her trip... Chris is a little brown bear. No one knows, where and when he met Mishka, but for a long time they are together (excluding her current trip). However, best friends are important too. John is Chris' best friend. Once walking with his friend, John gave Chris the following problem: At the infinite horizontal road of width $ w $ , bounded by lines $ y=0 $ and $ y=w $ , there is a bus moving, presented as a convex polygon of $ n $ vertices. The bus moves continuously with a constant speed of $ v $ in a straight $ Ox $ line in direction of decreasing $ x $ coordinates, thus in time only $ x $ coordinates of its points are changing. Formally, after time $ t $ each of $ x $ coordinates of its points will be decreased by $ vt $ . There is a pedestrian in the point $ (0,0) $ , who can move only by a vertical pedestrian crossing, presented as a segment connecting points $ (0,0) $ and $ (0,w) $ with any speed not exceeding $ u $ . Thus the pedestrian can move only in a straight line $ Oy $ in any direction with any speed not exceeding $ u $ and not leaving the road borders. The pedestrian can instantly change his speed, thus, for example, he can stop instantly. Please look at the sample note picture for better understanding. We consider the pedestrian is hit by the bus, if at any moment the point he is located in lies strictly inside the bus polygon (this means that if the point lies on the polygon vertex or on its edge, the pedestrian is not hit by the bus). You are given the bus position at the moment $ 0 $ . Please help Chris determine minimum amount of time the pedestrian needs to cross the road and reach the point $ (0,w) $ and not to be hit by the bus.

The first line of the input contains four integers $ n $ , $ w $ , $ v $ , $ u $ ( $ 3

Print the single real $ t $ — the time the pedestrian needs to croos the road and not to be hit by the bus. The answer is considered correct if its relative or absolute error doesn't exceed $ 10^{-6} $ .

Following image describes initial position in the first sample case: